Regel zu Stamm- und Integralfunktion
- Jede Integralfunktion von f über [a;b] ist auch auf [a;b] eine Stammfunktion
- Wenn eine Stammfunktion F von f mindestens eine Nullstelle in [a;b] besitzt, dann ist F eine Integralfunktion von f über [a;b].
- Wenn eine Stammfunktion F von f keine Nullstelle in [a;b] besitzt, dann ist F keine Integralfunktion von f über [a;b].
Symmetrie von Integralfunktion
gegeben ist die Funktion f(x) und die zugehörige Integralfunktion I(x)
- Wenn f(x) symmetrisch bzgl. eines Punkts
 ist, dann ist I(x) symmetrisch bzgl. der Achse
ist, dann ist I(x) symmetrisch bzgl. der Achse 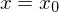 . Liegt das Symmetriezentrum von f nicht auf der x-Achse dann weist I(x) keine Symmetrie auf.
. Liegt das Symmetriezentrum von f nicht auf der x-Achse dann weist I(x) keine Symmetrie auf. - Wenn f(x) symmetrisch bzgl. der Achse
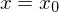 ist, dann ist I(x) symmetrisch bzgl. des Punktes
ist, dann ist I(x) symmetrisch bzgl. des Punktes 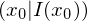
Extrema von Integralfunktionen
Eine Integralfunktionen:
- besitzt dort relative Minima, wo die Integrandenfunktion Nullstellen ungerader Ordnung besitzt -> der Graph stößt von unten nach oben durch die x-Achse
- besitzt dort relative Maxima, wo die Integrandenfunktion Nullstellen ungerader Ordnung besitzt -> der Graph stößt von oben nach unten durch die x-Achse
Krümmungsverhalten von Integralfunktionen
Eine Integralfunktion
- ist überall dort rechtssgekrümmt, wo f'(x) negativ ist -> der Graph der Integrandenfunktion fällt also streng monoton.
- ist überall dort linkssgekrümmt, wo f'(x) positiv ist -> der Graph der Integrandenfunktion steigt also streng monoton.
Uneigentliche Integrale 2.Art
Es liegen endliche Integrationsgrenzen vor, jedoch strebt die Integrandenfunktion an den Integrationsgrenzen ins Unendlich (z.B. Polstellen)
1.Fall Funktion ist im geschlossen Intervall [a;b[ integrierbar
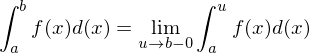
2.Fall Funktion ist im geschlossen Intervall ]a;b[ integrierbar

a besitzt z.B. eine Polstelle
1.Fall Funktion ist im geschlossen Intervall [a;b[ integrierbar
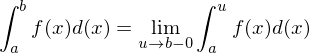
2.Fall Funktion ist im geschlossen Intervall ]a;b[ integrierbar

a besitzt z.B. eine Polstelle
Extremwertaufgaben - Vorgehensweise
1. Variable/ Größe feststellen die zu maximieren bzw. zu minimieren ist
2. Nebenbedingungen aus dem Text herauslesen und in Verbindung mit der Variable der Zielfunktion bringen. Wenn es im Text n Variablen gibt, dann wird es n-1 Nebenbedingung geben -> n-1 Gleichungen mit n Unbekannten
3. Gleichung mit einer einzigen Variable aufstellen und sinnvollen Definitionsbereich festlegen
4. Bestimmen der absoluten Maxima bzw. Minima -> Randextrema
2. Nebenbedingungen aus dem Text herauslesen und in Verbindung mit der Variable der Zielfunktion bringen. Wenn es im Text n Variablen gibt, dann wird es n-1 Nebenbedingung geben -> n-1 Gleichungen mit n Unbekannten
3. Gleichung mit einer einzigen Variable aufstellen und sinnvollen Definitionsbereich festlegen
4. Bestimmen der absoluten Maxima bzw. Minima -> Randextrema
Flashcard set info:
Author: JamesBond007
Main topic: Mathematik
Topic: Integralrechnung
Published: 07.11.2013
Card tags:
All cards (23)
no tags



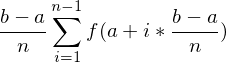



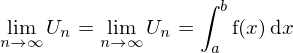


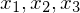 die zwischen a und b liegende Nullstellen einer integrierbaren Funktion f, so gilt für die Fläche A unter der Funktion f, die durch die Gerade x=a und x=b begrenzt wird.
die zwischen a und b liegende Nullstellen einer integrierbaren Funktion f, so gilt für die Fläche A unter der Funktion f, die durch die Gerade x=a und x=b begrenzt wird. 
 als Schnittpunkte der beiden Graphen so gilt für die eingeschlossene Fläche:
als Schnittpunkte der beiden Graphen so gilt für die eingeschlossene Fläche: 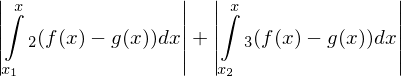

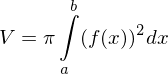
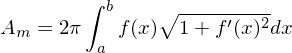
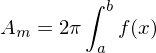 Umfang einer "einzelnen" Scheibe des Rotationsköpers
Umfang einer "einzelnen" Scheibe des Rotationsköpers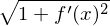

 c,x in [a;b] ist differenzierbar
c,x in [a;b] ist differenzierbar
 bezeichnet.
bezeichnet.
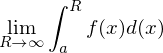

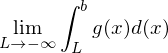
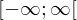
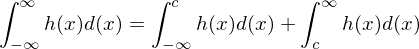
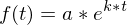

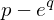 )
)
