Work Energy Theorem
Energy is conserved, thus
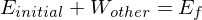 .
.
Use if possible whenever the problem calls for a distance and not a time.
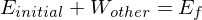 .
.Use if possible whenever the problem calls for a distance and not a time.
Moment of Inertia, I
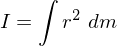
where dm is an infinitesimal mass element. Some common ones are given on the test, and most others can be found with the parallel axis theorem.
Parallel Axis Theorem
If you wish to know the moment of inertia about an axis parallel to the axis of the center of mass:
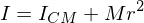
where r is the distance FROM THE CoM, not the radius.
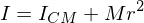
where r is the distance FROM THE CoM, not the radius.
The Lagrangian
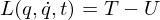
where T is the kinetic energy and U is the potential. Notice the minus sign, very important.
Euler-Lagrange Equations (generates the equations of motion)

where
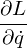 is the so call conjugate momentum to q.
is the so call conjugate momentum to q.Hamiltonian
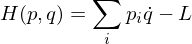
where L is the Lagrangian. If the potential U doesn't explictly depend upon time or velocity though, you can simply write
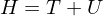
Classifications of Orbits
E > 0: hyperbolic orbit
E = 0: parabolic
E < 0; elliptical
E =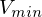 : circular
: circular
E = 0: parabolic
E < 0; elliptical
E =
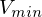 : circular
: circular Keplar's Laws
I. Planets follow elliptical orbits
II. Planets sweep out equal areas in equal times. Conservation of aerial velocity.
III. If T is the period of an orbit, and a is a semimajor axis of the orbit, then:
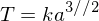
with k the same for all planets.
II. Planets sweep out equal areas in equal times. Conservation of aerial velocity.
III. If T is the period of an orbit, and a is a semimajor axis of the orbit, then:
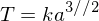
with k the same for all planets.
Normal Modes
Find the equation of motion using Lagrangian, then write in matrix form. With the matrix written, set the determinant to 0 and solve. Should always get one solution which looks like a regular spring 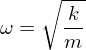 and one that is greater.
and one that is greater.
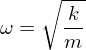 and one that is greater.
and one that is greater. Stokes Theorem
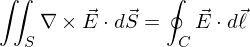
where \vec{E} is a general vector field and \vec{S] is the surface with direction given by its normal.
Conductors
Potential is always constant throughout a conductor. Net electric field inside is always 0. Charge is always on surface.
Parallel plate capacitance
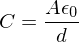
where A is the area of the plates and d is their separation. This is derived using the approximation that
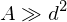 .
.Cyclotron Motion
Centripetal force equals the force of the magnetic field on the particle.
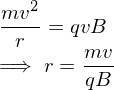
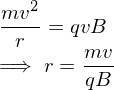
Faraday's Law
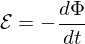
where
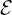 is the electromotive force (electrical potential) and
is the electromotive force (electrical potential) and 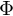 is the magnetic flux through an unclosed surface (
is the magnetic flux through an unclosed surface (  ).
).Inductance of a solenoid

where N is the total number of terms, A is the cross sectional area of the solenoid, and
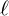 is an arbitrary length scale.
is an arbitrary length scale. Dipole Moments (E and M)
Electrical Dipole Moment
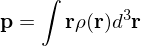
For point charges this reduces to
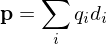 where
where 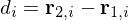 is the displacement vector.
is the displacement vector.
Magnetic Dipole Moment
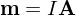
where A is the area with direction of the normal to the surface.
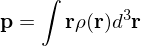
For point charges this reduces to
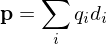 where
where 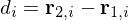 is the displacement vector.
is the displacement vector. Magnetic Dipole Moment
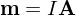
where A is the area with direction of the normal to the surface.
Potential and Torque of Dipole
Torque = (dipole moment) x (field)
Potential =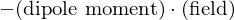
I wrote it this way so it works for both magnetic and electric dipoles.
Potential =
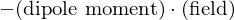
I wrote it this way so it works for both magnetic and electric dipoles.
Wave Equation
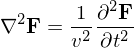
where F is any vector field. This has nice plane wave solutions for light where
 :
:
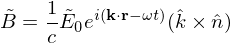
This also tells you that B is always perpendicular to E and usually smaller in amplitude (1/c is small).
Poynting vector
Tells you the flux of energy.
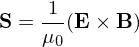
The intensity of radiation is just the time average of S; the sinusoids squared average to 1/2:
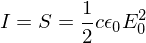
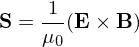
The intensity of radiation is just the time average of S; the sinusoids squared average to 1/2:
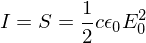
Index of refraction

where n is the index of refraction. Essentially slows the phase velocity down by a factor of 1/n.
Malus's Law

where
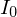 is the intensity of the light incident on the polarizer, and
is the intensity of the light incident on the polarizer, and 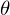 is the angle of the light's polarization with respect to the polarizer(i.e., let the light be polarized at
is the angle of the light's polarization with respect to the polarizer(i.e., let the light be polarized at 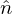 and the polarizer be
and the polarizer be 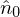 , then
, then 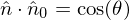 )
)Note this implies that for unpolarized light incident on a polarizer, you must average
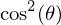 over all angles. This means 1/2 of the intensity of unpolarized light gets through.
over all angles. This means 1/2 of the intensity of unpolarized light gets through.Brewster's Angle
The angle at which light is completely polarized to the incident plane on a surface whose index of refraction is different from the current medium:


Maxima and Minima of a double slit
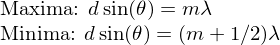
Remember to tell the difference that at
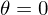 must be a maxima, which means that the right hand side must be an integer for maxima (0 isn't a half integer).
must be a maxima, which means that the right hand side must be an integer for maxima (0 isn't a half integer). Power radiated by an accelerating point charge
Called the Larmor formula, it says

where a is the acceleration. The constant of proportionality is not needed.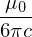 if you must know.
if you must know.

where a is the acceleration. The constant of proportionality is not needed.
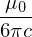 if you must know.
if you must know. Magnetic field of a solenoid

for an infinite solenoid along z with n turns per length.
Magnetic field of toroid
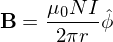
for N total turns. This is independent of the cross-section shape or area of the toroid and always holds for a toroid.
Power of an oscillating dipole
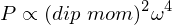
where dip mom represents either the magnetic or electric dipole moments and omega is the frequency of oscillation. The magnetic power has an extra factor of
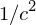 meaning that the electric dipole dominates the power term.
meaning that the electric dipole dominates the power term. Kirchhoff's Rules
I. The sum of the currents flowing into every node must be zero.
II. The sum of the voltages across any closed loop must be zero.
II. The sum of the voltages across any closed loop must be zero.
Optical path length
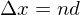
where n is the index of refraction. This is what introduces a phase difference between two waves, one in a vacuum and another in a medium with index of refraction n, when they recombine. The vacuum wave travels d, and the medium wave travels nd.
Phase shift when light reflects off boundary between two regions of different index of refraction
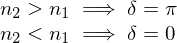
The Raylaigh Criterion for circular aperture
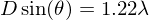
where D is the diameter of the hole. This basically just tells you that the angular separation between two objects seen through a hole must be greater than
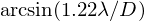 for them to appear as separate objects through the hole.
for them to appear as separate objects through the hole. Constructive interference vs destructive
Constructive occurs when there is an overall phase shift of 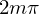 for some m, while destructive occurs when the phase shift is
for some m, while destructive occurs when the phase shift is 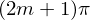 for some m.
for some m.
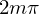 for some m, while destructive occurs when the phase shift is
for some m, while destructive occurs when the phase shift is 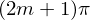 for some m.
for some m. Bragg diffraction
Maxima occur at 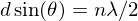
where theta is the angle of the incident X-rays wrt the plane of the crystal. Similar to double slit fomula, but the X-rays must traverse the distance between the two layers twice, hence the extra factor of 2.
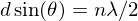
where theta is the angle of the incident X-rays wrt the plane of the crystal. Similar to double slit fomula, but the X-rays must traverse the distance between the two layers twice, hence the extra factor of 2.
Snell's Law
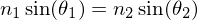
where both angles are taken from the normal to the surface of refraction.
Focal length equation in Geometric Optics

where f is the focal length of the lens, s is the position of the object, and s' the position of the image.
Magnification

where s' is the position of the image and s is the position of the object wrt to the lens.
Rayleigh Scattering
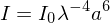
where I is the intensity of scattered light,
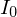 is the intensity of the light we see and
is the intensity of the light we see and  is the particle size. This effect is responsible for the blue sky and the red sunset.
is the particle size. This effect is responsible for the blue sky and the red sunset. Doppler Effect (sound)
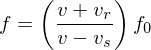
where v is the velocity of the wave,
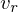 is the velocity of the receiver, and
is the velocity of the receiver, and 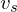 is the velocity of the source. The signs of
is the velocity of the source. The signs of 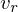 is positive if the motion is toward the source, and
is positive if the motion is toward the source, and 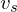 is positive if the source is moving toward the receiver.
is positive if the source is moving toward the receiver. Entropy

where
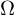 is the number of possible microstates and k is Boltzmann's constant.
is the number of possible microstates and k is Boltzmann's constant.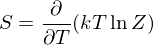
where T is temperature.
If its reversible and all you care about is the change in entropy:
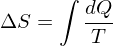
Equipartition Theorem
Every degree of freedom contributes 1/2 kT to the internal energy and thus 1/2 k to the heat capacity.
Generally at low energies most of the degrees of freedom freeze out leaving 3/2 kT. At very high energies for a diatomic molecule, it caps at 7/2 kT.
Generally at low energies most of the degrees of freedom freeze out leaving 3/2 kT. At very high energies for a diatomic molecule, it caps at 7/2 kT.
The Three Laws of Thermodynamics
1. Energy cannot be created or destroyed:
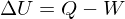
where U is the internal energy, Q is heat, W work.
2. There is no process who's sole effect is to transfer heat from a hot body to a cold body. Another way to put it is that no engine can convert energy from a heat reservoir entirely into mechanical energy.
Mathematically: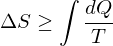
3. Entropy is zero at absolute zero.
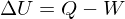
where U is the internal energy, Q is heat, W work.
2. There is no process who's sole effect is to transfer heat from a hot body to a cold body. Another way to put it is that no engine can convert energy from a heat reservoir entirely into mechanical energy.
Mathematically:
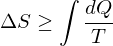
3. Entropy is zero at absolute zero.
Reversible Process
A slow process that creates no extra entropy (the total change between the system and the outside is 0). In a reversible process the following is true:
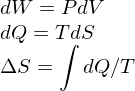
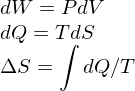
Quasistatic
A process so slow its considered constantly in equilibrium. A reversible process is always quasistatic.
Work done goes as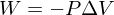 if P constant, or
if P constant, or 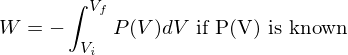 .
.
Work done goes as
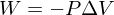 if P constant, or
if P constant, or 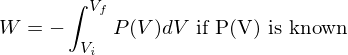 .
. Isothermal
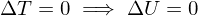 .
.If taken to be a slow process, work can be calculated with quasistatic work.
Adiabatic
No heat is exchanged, 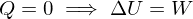
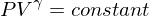 which can be used to solve the work using quasistatic work.
which can be used to solve the work using quasistatic work. 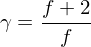 where f is the degrees of freedom.
where f is the degrees of freedom.
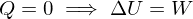
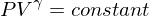 which can be used to solve the work using quasistatic work.
which can be used to solve the work using quasistatic work. 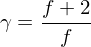 where f is the degrees of freedom.
where f is the degrees of freedom.Temperature and Pressure
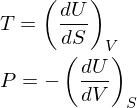
both of which come straight from the thermodynamic identity. If that's easier to memorize than skip this.
Heat Capacity
There is two, defined for either constant volume or pressure:
 .
.
An important side note, for ideal gases always.
always.
 .
.An important side note, for ideal gases
 always.
always.Fermi-Dirac Distribution
The partition function for fermions looks like
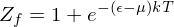
which gives an occupancy (average number of particles) of
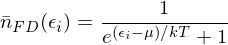
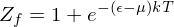
which gives an occupancy (average number of particles) of
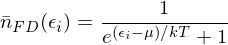
Bose-Einstein Distribution
For bosons the partition function looks like
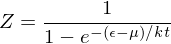
which gives an occupancy
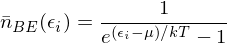
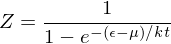
which gives an occupancy
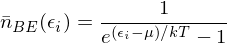
Energy of a free particle
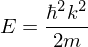
which should be easy to remember as
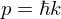 and the normal energy formula for a free particle
and the normal energy formula for a free particle 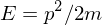
Ground State Energy for Hyrdrogen

13.6 is super important, but the form of the equation is important for Hydrogen-like atoms.
Energy of excited states of hydrogen
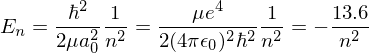
where the second one is substituting in the definition of the Bohr radius and the last number is only valid for Hydrogen.
First Order Correction to a perturbed Hamiltonian
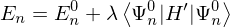
where
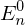 is the unperturbed nth Energy, similarly for the wavefunctions while lambda is the perturbation parameter..
is the unperturbed nth Energy, similarly for the wavefunctions while lambda is the perturbation parameter.. Lorentz Transformations
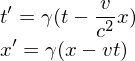
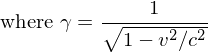
For the reverse transformations, change the sign of v and switch the primed with the unprimed.
Einstein velocity addition rule

where w is the speed an object in frame S, v is the speed of S', and u is the speed of the object in the S' frame.
Relativistic Kinetic Energy
The rest energy is 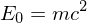 and the total energy is given by
and the total energy is given by 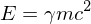 which implies that the kinetic energy is
which implies that the kinetic energy is

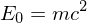 and the total energy is given by
and the total energy is given by 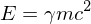 which implies that the kinetic energy is
which implies that the kinetic energy is 
Energy-Momentum Invariance
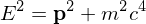 is invariant (the same in all inertial reference frames) and conserved.
is invariant (the same in all inertial reference frames) and conserved. Invariant Dot Product
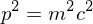
where p is the momentum 4-vector. SUPER USEFUL for calculations.
Boost Matrix along x-axis
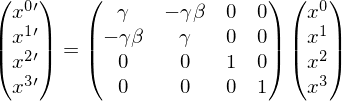
which reduces to the regular Lorentz transformations as long as you remember
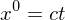 . NOTE, to get the inverse transformation you just need to change the signs of the off diagonal elements and switch the primes.
. NOTE, to get the inverse transformation you just need to change the signs of the off diagonal elements and switch the primes.Poison Distribution

where
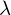 is the average amount of counts in a given interval.
is the average amount of counts in a given interval.Remember its
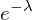 times a term of the power series for
times a term of the power series for 
It has error
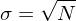 for large N.
for large N. Common and useful constants
13.6 eV - Binding Energy of Hydrogen
.5 MeV/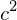 - Mass of Electron (Proton is ~2000 times this, 1 GeV
- Mass of Electron (Proton is ~2000 times this, 1 GeV
1.22 - Rayleigh criterion coefficient for a circle aperture.
 - Wien displacement law constant
- Wien displacement law constant
2.7 K - T of cosmic microwave background
 - hc in the given units.
- hc in the given units.
.5 MeV/
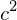 - Mass of Electron (Proton is ~2000 times this, 1 GeV
- Mass of Electron (Proton is ~2000 times this, 1 GeV1.22 - Rayleigh criterion coefficient for a circle aperture.
 - Wien displacement law constant
- Wien displacement law constant2.7 K - T of cosmic microwave background
 - hc in the given units.
- hc in the given units. Max energy of an electron emitted from photoabsorption (Photoelectric effect)
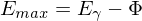
where
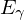 is the energy of the incident photon which is absorbed and
is the energy of the incident photon which is absorbed and 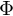 is the work function of the material.
is the work function of the material. Wavelength shift of light under Compton scattering
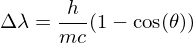
where
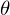 is the angle the photon is scattered at.
is the angle the photon is scattered at. Kartensatzinfo:
Autor: CoboCards-User
Oberthema: Physics
Thema: GRE
Schule / Uni: UC Santa Cruz
Ort: Santa Cruz, CA
Veröffentlicht: 20.10.2015
Schlagwörter Karten:
Alle Karten (111)
keine Schlagwörter




 is the normal force
is the normal force

 is the tangential velocity.
is the tangential velocity. 



 .
.








 .
.  .
.





















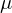 is the reduced mass. (
is the reduced mass. (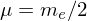 for positronium.)
for positronium.)




 is the peak wavelength emitted by a blackbody.
is the peak wavelength emitted by a blackbody. 



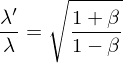

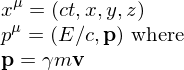

 is the driving frequency of the AC circuit.
is the driving frequency of the AC circuit. 