What is an affine connection?
An affine connection is a connection 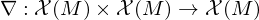
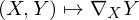
satisfying
i)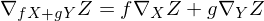
ii)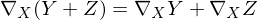
iii)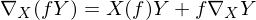
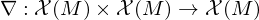
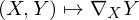
satisfying
i)
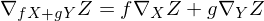
ii)
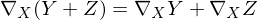
iii)
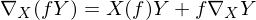
What is a Riemannian or Levi Civita connection?
An affine connection that also satisfies
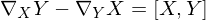 torsion-free
torsion-free
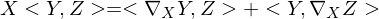
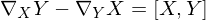 torsion-free
torsion-free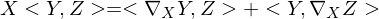
How is a differentiable manifold of dimension n defined?
A set M, a family of injective maps 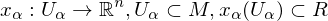 is open such that
is open such that
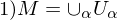
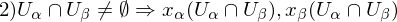 are open and
are open and 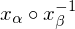 is differentiable
is differentiable  .
.
 there exists a maximal atlas {
there exists a maximal atlas {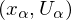 } relative to M
} relative to M
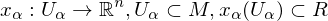 is open such that
is open such that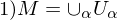
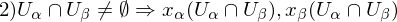 are open and
are open and 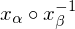 is differentiable
is differentiable 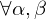 .
. there exists a maximal atlas {
there exists a maximal atlas {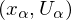 } relative to M
} relative to MHow is a Riemannian Metric defined?
As g or 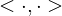 as an inner product,
as an inner product,
where an inner product is
-symmetric,
-linear and
-positive definite
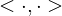 as an inner product,
as an inner product,where an inner product is
-symmetric,
-linear and
-positive definite
Let 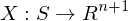 be a Vector field for
be a Vector field for 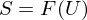 . When is X differentiable and how is
. When is X differentiable and how is 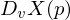 for
for 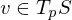 defined?
defined?
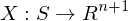 be a Vector field for
be a Vector field for 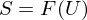 . When is X differentiable and how is
. When is X differentiable and how is 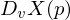 for
for 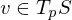 defined?
defined?X is differentiable if 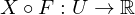 is differentiable.
is differentiable.
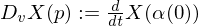
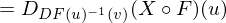
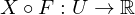 is differentiable.
is differentiable.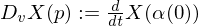
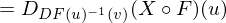
How was the covariant Derivative for two vector fields 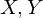 simply (firstly) calculated?
simply (firstly) calculated?
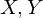 simply (firstly) calculated?
simply (firstly) calculated?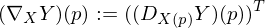
where
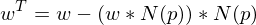
How is a topological space 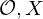 defined?
defined?
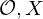 defined?
defined?We have a Family 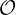 of open subsets of
of open subsets of 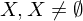 satisfying
satisfying
(T.1)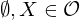
(T.2)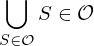
(T.3)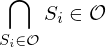 of finite i's
of finite i's
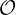 of open subsets of
of open subsets of 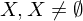 satisfying
satisfying(T.1)
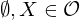
(T.2)
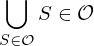
(T.3)
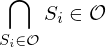 of finite i's
of finite i'sWhat is the algebraic Definition of a tangent vector at p?
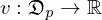 satisfying
satisfying(1)
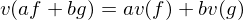
(2)
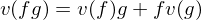
where
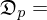 {diff. fcts. at p}
{diff. fcts. at p}An n-dimensional smooth manifold M is called orientable if
There exists a differentiable atlas 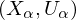 for M s.t.
for M s.t.
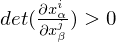 at p, for all p in
at p, for all p in 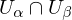
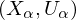 for M s.t.
for M s.t.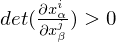 at p, for all p in
at p, for all p in 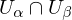
What is an Immersion?
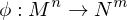 where
where 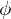 is differentiable is called an immersion if
is differentiable is called an immersion if 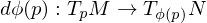 is injective
is injective 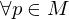
equivalently

What is an Embedding?
An Immersion 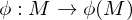 that is a homeomorphism
that is a homeomorphism 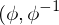 cont's)
cont's)
and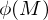 has the subspace topology induced from
has the subspace topology induced from 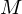 .
.
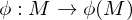 that is a homeomorphism
that is a homeomorphism 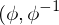 cont's)
cont's) and
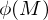 has the subspace topology induced from
has the subspace topology induced from 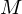 .
.What is an intrinsic quality?
A geometric quality that can be expressed only in terms of 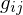 and its derivative function.
and its derivative function.
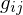 and its derivative function.
and its derivative function.What is the difference of an affine connection and the covariant derivative?
 is an affine connection as
is an affine connection as 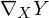 is the covariant derivative for the vector fields X and Y.
is the covariant derivative for the vector fields X and Y.Kartensatzinfo:
Autor: Yann-Paul
Oberthema: Mathematik
Thema: Differentialgeometrie123
Veröffentlicht: 15.11.2018
Schlagwörter Karten:
Alle Karten (40)
keine Schlagwörter



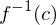 ,
, 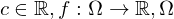 open.
open. 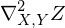

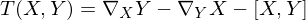
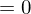 if connection is torsion free.
if connection is torsion free.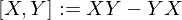 have?
have?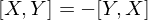
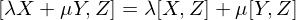
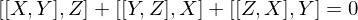 Jacobi Identity
Jacobi Identity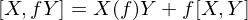 product rule
product rule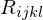 ?
?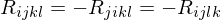 symmetries
symmetries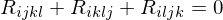 Bianchi identity
Bianchi identity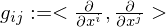
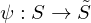 a local isometry?
a local isometry?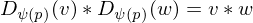
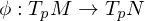 is an Isometry if
is an Isometry if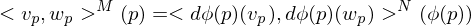
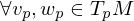
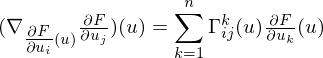
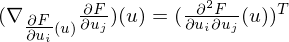
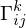 be calculated in terms of
be calculated in terms of 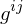 ?
?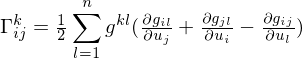
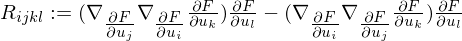
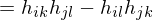
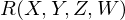 defined?
defined?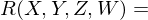
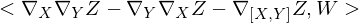
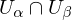 be connected. What do we know for M?
be connected. What do we know for M?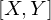 defined?
defined?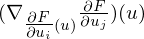 calculated?
calculated?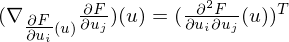
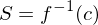 defined?
defined?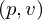 is called a tangent vector to
is called a tangent vector to  at
at 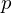 if
if 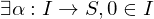 with
with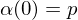
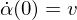
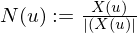 where
where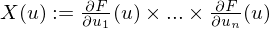
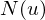 ?
?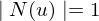
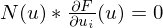
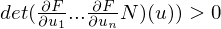
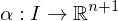 where
where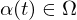
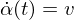
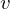 is any Vector.
is any Vector.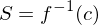 ,
, 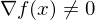 .
.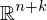
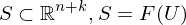 ,
,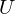 open,
open, 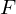 smooth and
smooth and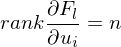 or
or 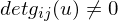
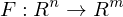
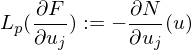
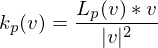
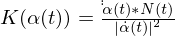
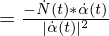
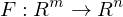
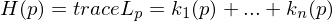
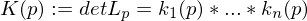
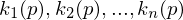
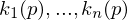 are the Eigenvalues of
are the Eigenvalues of  .
.