Wozu braucht man Simulation?
- wir wollen Simulation verwenden, um komplexe Probleme greifbar zu machen und sie einer Lösung zuzuführen
- Kerntechnologie, um Entwicklungsprozesse im Maschinenbau, in der Luft- und Raumfahrttechnik und in der Verfahrenstechnik zu unterstützen
- Bewertung des Produktionsprozesses mit Hilfe eines Modells in der virtuellen Welt
- Verständnis des Systems
- Entwicklung von Strategien zum Betrieb eines Systems
Beispiel für ein DA-System
Thermodynamisches System:
Differentielle Gleichungen: z.B. Bilanzgleichungen
Algebraische Gleichungen: z.B. Gleichungen für Reaktionsraten
Algebraische Variablen: z.B. Temperatur
Parameter: z.B. Reaktionskonstante
Pendel:
Differentielle Gleichungen: z.B. Geschwindigkeit
Algebraische Variablen: z.B. Position
Anfangswerte: z.B. Anfangsposition, Geschwindigkeit, etc.
Differentielle Gleichungen: z.B. Bilanzgleichungen
Algebraische Gleichungen: z.B. Gleichungen für Reaktionsraten
Algebraische Variablen: z.B. Temperatur
Parameter: z.B. Reaktionskonstante
Pendel:
Differentielle Gleichungen: z.B. Geschwindigkeit
Algebraische Variablen: z.B. Position
Anfangswerte: z.B. Anfangsposition, Geschwindigkeit, etc.
Bilanzierung von Massen bei der Modellierung allgemeiner thermodynamischer Systeme
Die Gesamtmassenbilanz und alle Stoffmassenbilanzen bilden gemeinsam ein Index-0 System. Durch numerische Fehler bei der Integration wird die Lösung dieses Systems im Allgemeinen nicht die Schließbedingung erfüllen. Alternativ werden die Gesamtmassenbilanz, die Schließbedingung und n−1 Einzelmassenbilanzen aufgestellt, wobei n die Anzahl der beteiligten Stoffe ist.
Nachteile explizites Euler-Verfahren
- Verfahren ist nicht A-stabil
- für große Zeitschritte wird keine stabile Lösung gefunden
Möglichkeiten um das Anfangswertproblem stabil zu lösen:
- Benutzung eines anderen numerischen Lösungsverfahrens (z.B. implizites Euler-Verfahren)
- Verkleinerung der Schrittweite
differentieller Index eines differentiell-algebraischen Systems
- die minimale Anzahl an Differentiationen, die auf Teile des Systems oder des Gesamtsystems angewandt werden müssen, um das DA-System in ein System gewöhnlicher Differentialgleichungen zu überführen
- ein System mit einem Index kleiner oder gleich eins liegt vor, wenn alle algebraischen Gleichungen nach allen algebraischen Variablen aufgelöst werden können
Indexreduktion
1. Zeitliche Ableitung der algebraischen Gleichungen
2. Einsetzen der differentiellen Gleichungen
3. Versteckte algebraische Gleichungen
4. Explizite Gleichung für jede algebraische Gleichung möglich?
2. Einsetzen der differentiellen Gleichungen
3. Versteckte algebraische Gleichungen
4. Explizite Gleichung für jede algebraische Gleichung möglich?
- Ja: Index-1 System aufstellen
- Nein: Erneutes Ableiten der algebraischen Gleichungen
Erklären Sie, wie man ohne mathematische Rechnung feststellen kann, ob ein DA-System einen Index größer 1 hat.
Sind die algebraischen Gleichungen eines DA-Systems nicht nach den algebraischen Variablen auflösbar, dann hat das System einen differentiellen Index größer Eins (Inzidenzmatrix der algebraischen Gleichungen hat nicht vollen Rang).
Sprungbedingung (hybrider Automat)
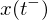 : bezeichnet den linksseitigen Grenzwert einer Variablen x am Zeitpunkt t, also den Wert vor dem Eintreten eines diskreten Ereignisses bei t
: bezeichnet den linksseitigen Grenzwert einer Variablen x am Zeitpunkt t, also den Wert vor dem Eintreten eines diskreten Ereignisses bei t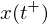 : bezeichnet den rechtsseitigen Grenzwert von x am Zeitpunkt t, also den Wert nach dem Eintreten eines diskreten Ereignisses
: bezeichnet den rechtsseitigen Grenzwert von x am Zeitpunkt t, also den Wert nach dem Eintreten eines diskreten EreignissesHybrider Automat
- Möglichkeit zur Modellierung hybrider Systeme
- hybride Systeme bestehen aus einem diskreten und einem kontinuierlichen Teil
- in Moden wird eine Differentialgleichung eingebettet, die kontinuierlichen Regler repräsentiert
- Übergang zwischen Moden ist diskret
Beispiel: elektrischer Schaltkreis
weist fast immer einen kontinuierlichen Verlauf von Strom und Spannung auf, wird aber zu diskreten Zeitpunkten durch schaltende Bauelemente (z.B. Transistoren) beeinflusst
Trajektorie
Für wachsende t beschreibt x(t) die Bahnkurve bzw. eine so genannte Trajektorie.
Phasenporträt: Trajektorien eines Systems für mehrere Anfangswerte im selben Diagramm
- dürfen Schlangenlinien fahren
- dürfen sich für verschiedene Anfangswerte nicht schneiden
- keine Sprünge, kein Knick
Phasenporträt: Trajektorien eines Systems für mehrere Anfangswerte im selben Diagramm
Indirekte Methode von Ljapunow
- Linearisierung um die Ruhelage
- es kann von den Realteilen der Eigenwerte auf das lokale Stabilitätsverhalten geschlossen werden
- Hartman-Grobman: Rückschluss vom linearisierten System auf das nichtlineare System ist nur zulässig, wenn die Matrix A keinen Eigenwert hat, dessen Realteil Null ist
Grenzzyklus und Attraktor
- Wenn für beliebige Startwerte (außer der instabilen Ruhelage) alle Trajektorien auf eine geschlossene Trajektorie zulaufen, ist diese der Grenzzyklus und in diesem Fall der Attraktor
- Attraktor: eine Untermenge des Zustandsraums, der sich Systemzustände in einem bestimmten Einzugsbereich annähern und die unter der Dynamik des nichtlinearen Systems nicht mehr verlassen wird
- Ruhelagen sind Spezialfälle von Attraktoren
Flashcard set info:
Author: CoboCards-User
Main topic: Simulationstechnik RWTH
Topic: AVT
Published: 25.05.2018
Card tags:
All cards (82)
no tags




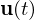 .
.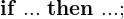
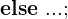
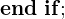
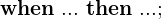
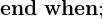

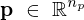 eines Systems
eines Systems 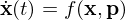 .
.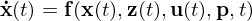
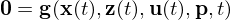
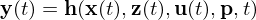
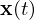 : differentielle Variablen (Zustände)
: differentielle Variablen (Zustände)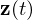 : algebraische Variablen
: algebraische Variablen 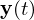 : Ausgänge
: Ausgänge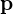 : Parameter
: Parameter

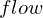 ) werden zu Null addiert.
) werden zu Null addiert.
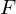 , Drehmoment
, Drehmoment 
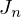 , Massenfluss
, Massenfluss 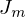 , Wärmefluss
, Wärmefluss 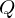
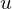
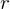 , Drehwinkel
, Drehwinkel 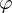
 , Temperatur
, Temperatur 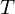

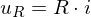
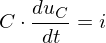
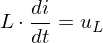
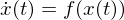

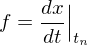

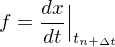

 PDF (oder UPDF) ist und
PDF (oder UPDF) ist und 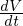 NSDF ist
NSDF ist


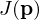 : Gütemaß
: Gütemaß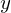 : Ausgang
: Ausgang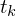 : Messzeiten
: Messzeiten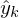 : Messwerte
: Messwerte


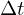
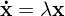
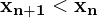


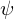 : zu bilanzierende Größe
: zu bilanzierende Größe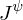 : Fluss
: Fluss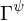 : Quelle/ Senke
: Quelle/ Senke

 Kantengewicht:
Kantengewicht: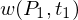 : Anzahl der zur Aktivierung der Transition notwendigen Token
: Anzahl der zur Aktivierung der Transition notwendigen Token : Zahl der Token nach der Transition
: Zahl der Token nach der Transition
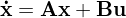 und
und 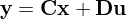 für konstante Eingänge eine eindeutige Ruhelage besitzt?
für konstante Eingänge eine eindeutige Ruhelage besitzt?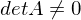
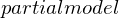 und
und 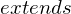 in Modelica
in Modelica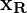 bleibt die Lösung des Systems immer in der
bleibt die Lösung des Systems immer in der  -Umgebung, überschreitet also nie den äußeren Kreis
-Umgebung, überschreitet also nie den äußeren Kreis 


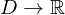
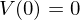
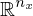 )
)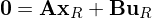

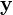 (Sensitivitätsmatrix der Zustände
(Sensitivitätsmatrix der Zustände 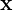 analog):
analog):
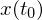 des Zustandsraums als Einzugsbereich bezeichnet, aus denen die Trajektorien x(t) für t → ∞ gegen die Ruhelage streben
des Zustandsraums als Einzugsbereich bezeichnet, aus denen die Trajektorien x(t) für t → ∞ gegen die Ruhelage streben