Simulation
- Verfahren zur Nachbildung eines Systems mit seinen dynamischen Prozessen in einem experimentierbaren Modell, um zu Erkenntnissen zu gelangen, die auf die Wirklichkeit übertragbar sind
- Vorbereiten, Durchführen und Auswerten gezielter Experimente mit einem Simulationsmodell
Wozu braucht man Simulation?
- wir wollen Simulation verwenden, um komplexe Probleme greifbar zu machen und sie einer Lösung zuzuführen
- Kerntechnologie, um Entwicklungsprozesse im Maschinenbau, in der Luft- und Raumfahrttechnik und in der Verfahrenstechnik zu unterstützen
- Bewertung des Produktionsprozesses mit Hilfe eines Modells in der virtuellen Welt
- Verständnis des Systems
- Entwicklung von Strategien zum Betrieb eines Systems
Hilfskonstrukte zur Beschreibung von Schaltfunktionen in Modelica
1. if-Bedingung:
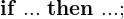
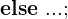
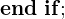
2. when-Bedingung:
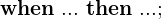
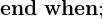
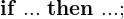
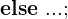
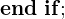
2. when-Bedingung:
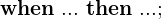
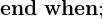
Allgemeine Form für jede Art der Zustandsraumdarstellung - Durch welche Methode sind Umformungen zwischen den Zustandsraumdarstellungen möglich?

Ereignisdiskretes System
Werte der Zustände sind diskret und ändern sich ausschließlich als Folge von externen oder internen Ereignissen (keine Zeitabhängigkeit)
- Petri-Netz
- Endlicher Automat
Wie bezeichnet man Systeme, deren Verhalten sehr stark von den Anfangswerten abhängt, so dass Vorhersagen über längere Zeit nicht möglich sind?
Chaotisches System
Bifurkation
Änderung des qualitativen Verhaltens des Systems durch die Änderung der Parameter 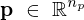 eines Systems
eines Systems 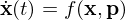 .
.
Beispiel: Anzahl an Ruhelagen, Stabilität einer oder mehrerer Ruhelagen
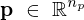 eines Systems
eines Systems 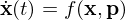 .
.Beispiel: Anzahl an Ruhelagen, Stabilität einer oder mehrerer Ruhelagen
Allgemeine Gleichungen für ein differentiell-algebraisches System
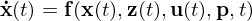
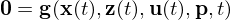
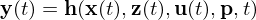
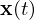 : differentielle Variablen (Zustände)
: differentielle Variablen (Zustände)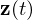 : algebraische Variablen
: algebraische Variablen 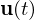 : Eingänge
: Eingänge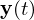 : Ausgänge
: Ausgänge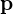 : Parameter
: ParameterDie zusätzlichen algebraischen Gleichungen schränken den Lösungsraum des differentiellen Systems sowie dessen Anfangswerte ein.


Beispiel für ein DA-System
Thermodynamisches System:
Differentielle Gleichungen: z.B. Bilanzgleichungen
Algebraische Gleichungen: z.B. Gleichungen für Reaktionsraten
Algebraische Variablen: z.B. Temperatur
Parameter: z.B. Reaktionskonstante
Pendel:
Differentielle Gleichungen: z.B. Geschwindigkeit
Algebraische Variablen: z.B. Position
Anfangswerte: z.B. Anfangsposition, Geschwindigkeit, etc.
Differentielle Gleichungen: z.B. Bilanzgleichungen
Algebraische Gleichungen: z.B. Gleichungen für Reaktionsraten
Algebraische Variablen: z.B. Temperatur
Parameter: z.B. Reaktionskonstante
Pendel:
Differentielle Gleichungen: z.B. Geschwindigkeit
Algebraische Variablen: z.B. Position
Anfangswerte: z.B. Anfangsposition, Geschwindigkeit, etc.
Fluss- und Potentialvariablen
Potentialvariablen werden beim Verkoppeln gleich gesetzt, Flussvariablen (Modelica-Schlüsselwort: 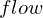 ) werden zu Null addiert.
) werden zu Null addiert.
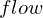 ) werden zu Null addiert.
) werden zu Null addiert.Beispiele für Flussvariablen
elektrische Systeme: Stromfluss 
mechanische Systeme: Kraft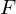 , Drehmoment
, Drehmoment 
thermodynamische Systeme: Stofffluss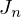 , Massenfluss
, Massenfluss 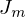 , Wärmefluss
, Wärmefluss 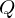

mechanische Systeme: Kraft
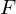 , Drehmoment
, Drehmoment 
thermodynamische Systeme: Stofffluss
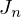 , Massenfluss
, Massenfluss 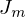 , Wärmefluss
, Wärmefluss 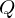
Beispiele für Potentialvariablen
elektrische Systeme: Spannung 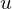
mechanische Systeme: Position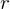 , Drehwinkel
, Drehwinkel 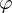
thermodynamische Systeme: Druck , Temperatur
, Temperatur 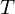
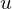
mechanische Systeme: Position
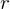 , Drehwinkel
, Drehwinkel 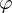
thermodynamische Systeme: Druck
 , Temperatur
, Temperatur 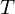
Bilanzierung von Massen bei der Modellierung allgemeiner thermodynamischer Systeme
Die Gesamtmassenbilanz und alle Stoffmassenbilanzen bilden gemeinsam ein Index-0 System. Durch numerische Fehler bei der Integration wird die Lösung dieses Systems im Allgemeinen nicht die Schließbedingung erfüllen. Alternativ werden die Gesamtmassenbilanz, die Schließbedingung und n−1 Einzelmassenbilanzen aufgestellt, wobei n die Anzahl der beteiligten Stoffe ist.
Allgemeine Bilanzgleichung für Energie

a: Zeitliche Änderung der Energie im Bilanzraum (Speicherterm)
b: Enthalpieströme (Strom)
c: Wärmeströme (Strom)
d: Technische Arbeit (Strom)
e: Volumenänderungsarbeit (Strom)
Kann man ein lineares, zeitvariantes System in Zustandsraumdarstellung immer zu einem linearen, zeitinvarianten System umformen?
Nur in Spezialfällen, die im Rahmen der Simulationstechnik-Vorlesung nicht betrachtet werden.
Ist ein System über- oder unterbestimmt?
Freiheitsgradanalyse:
Variablen - Gleichungen = Freiheitsgrade
Freiheitsgrade geben an, wieviele Variablen mehr als Gleichungen im System vorhanden sind.
f > 0: unterbestimmt
f < 0: überbestimmt
Variablen - Gleichungen = Freiheitsgrade
Freiheitsgrade geben an, wieviele Variablen mehr als Gleichungen im System vorhanden sind.
f > 0: unterbestimmt
f < 0: überbestimmt
Teilsystembezeichnung sowie die jeweils benötigte Bauteilgleichung eines elektrischen Systems
Widerstand (Speicher- oder Verknüpfungssystem):
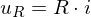
Kondensator (Speichersystem):
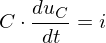
Spule (Speichersystem):
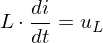
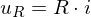
Kondensator (Speichersystem):
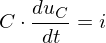
Spule (Speichersystem):
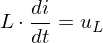
Gleichungen für das explizite und das implizite Euler-Verfahren für das allgemeine System 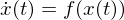
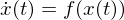
Explizites Euler-Verfahren:

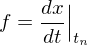
Implizites Euler-Verfahren:

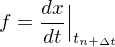
Auswertung der Funktion zu unterschiedlichen Zeitpunkten.

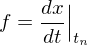
Implizites Euler-Verfahren:

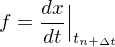
Auswertung der Funktion zu unterschiedlichen Zeitpunkten.
Nachteile explizites Euler-Verfahren
- Verfahren ist nicht A-stabil
- für große Zeitschritte wird keine stabile Lösung gefunden
Möglichkeiten um das Anfangswertproblem stabil zu lösen:
- Benutzung eines anderen numerischen Lösungsverfahrens (z.B. implizites Euler-Verfahren)
- Verkleinerung der Schrittweite
Konzentrierte und verteilte Systeme
- Konzentrierte Systeme sind ortsunabhängig (d.h. Beschreibung mittels gewöhnlicher Differentialgleichungen und algebraischer Gleichungen)
- Verteilte Systeme sind ortsabhängig (d.h. Beschreibung mittels partieller Differentialgleichungen
Gegeben ist ein System der Form 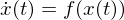 mit Dimension 2. Kann in dem System Chaos auftreten?
mit Dimension 2. Kann in dem System Chaos auftreten?
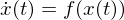 mit Dimension 2. Kann in dem System Chaos auftreten?
mit Dimension 2. Kann in dem System Chaos auftreten? Nein, denn damit das gegebene System chaotisch sein kann, muss
seine Dimension echt größer als 2 (also mindestens 3) sein.
seine Dimension echt größer als 2 (also mindestens 3) sein.
LaSalle Theorem
- Wird verwendet um zu untersuchen, ob die Ruhelage des Systems nicht nur stabil, sondern auch asymptotisch stabil ist
- kann angewendet werden, wenn die Ljapunow Funktion
 PDF (oder UPDF) ist und
PDF (oder UPDF) ist und 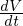 NSDF ist
NSDF istAllgemeines Parameterschätzproblem nach der Methode der kleinsten Fehlerquadrate für dynamische Systeme mit einem (skalaren) Ausgang

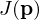 : Gütemaß
: Gütemaß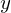 : Ausgang
: Ausgang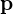 : Parameter
: Parameter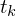 : Messzeiten
: Messzeiten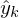 : Messwerte
: MesswerteVor- und Nachteile des impliziten Euler-Verfahrens
+ höhere Genauigkeit als beim expliziten Euler-Verfahren
+ Stabilität unabhängig von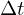
- es muss ein Gleichungssystem gelöst werden, um die Lösung zum neuen Zeitpunkt zu berechnen
+ Stabilität unabhängig von
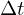
- es muss ein Gleichungssystem gelöst werden, um die Lösung zum neuen Zeitpunkt zu berechnen
Dahlquistsche Testgleichung und Bedingungen zur Untersuchung der Stabilität eines numerischen Integrationsverfahrens
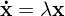
Damit ein Verfahren A-stabil ist, muss ∀ λ mit Re(λ)<0 und
∀ Schrittweiten ∆t gelten:
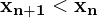
Allgemeine Bilanzgleichung für ein thermodynamisches System

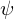 : zu bilanzierende Größe
: zu bilanzierende Größe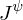 : Fluss
: Fluss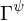 : Quelle/ Senke
: Quelle/ SenkeTypen von Teilsystemen bei der strukturierten Systemdarstellung
Speichersysteme, Verknüpfungssysteme
Womit bestimmt man analytisch, ob ein System vollständig spezifiziert ist?
Freiheitsgradanalyse
Petri-Netz
 Kantengewicht:
Kantengewicht:-
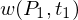 : Anzahl der zur Aktivierung der Transition notwendigen Token
: Anzahl der zur Aktivierung der Transition notwendigen Token -
 : Zahl der Token nach der Transition
: Zahl der Token nach der Transition
- ungerichtete oder gerichtete Kanten
Verhalten hybrider Systeme und Beispiele für ein
hybrides System
hybrides System
- diskretes und kontinuierliches Verhalten
- Bsp.: elektrischer Schaltkreis, springender Ball, Thermostat, Wetter, Auto
Verteilung von Parameterwerten gemäß dem Latin hypercube sampling

Zwei mögliche Lösungen für die Verteilung von Parameterwerten im Parameterraum (insgesamt gibt es 6! = 720 korrekte Lösungen)
Klassen von autonomen kontinuierlichen dynamischen Systemen
- nichtlineares zeitvariantes System
- lineares zeitvariantes System
- nichtlineares zeitinvariantes System
- lineares zeitinvariantes System
Kirchoff’schen Regeln
Es werden
n−1 Knotengleichungen und
z−(n−1) Maschengleichungen
benötigt.
(z: Zweige)
n−1 Knotengleichungen und
z−(n−1) Maschengleichungen
benötigt.
(z: Zweige)
Welche Bedingung muss gelten, damit ein lineares System mit 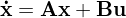 und
und 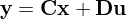 für konstante Eingänge eine eindeutige Ruhelage besitzt?
für konstante Eingänge eine eindeutige Ruhelage besitzt?
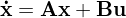 und
und 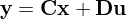 für konstante Eingänge eine eindeutige Ruhelage besitzt?
für konstante Eingänge eine eindeutige Ruhelage besitzt?A muss vollen Rang haben bzw. 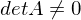
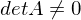
Arten von Freiheitsgraden
- konstruktionsbedingte Freiheitsgrade
- betriebsbedingte Freiheitsgrade
Was muss für ein autonomes System gelten, damit das zugehörige nicht-autonome System bei konstanten Eingängen stabil ist?
Das autonome System muss stabil sein.
differentieller Index eines differentiell-algebraischen Systems
- die minimale Anzahl an Differentiationen, die auf Teile des Systems oder des Gesamtsystems angewandt werden müssen, um das DA-System in ein System gewöhnlicher Differentialgleichungen zu überführen
- ein System mit einem Index kleiner oder gleich eins liegt vor, wenn alle algebraischen Gleichungen nach allen algebraischen Variablen aufgelöst werden können
Indexreduktion
1. Zeitliche Ableitung der algebraischen Gleichungen
2. Einsetzen der differentiellen Gleichungen
3. Versteckte algebraische Gleichungen
4. Explizite Gleichung für jede algebraische Gleichung möglich?
2. Einsetzen der differentiellen Gleichungen
3. Versteckte algebraische Gleichungen
4. Explizite Gleichung für jede algebraische Gleichung möglich?
- Ja: Index-1 System aufstellen
- Nein: Erneutes Ableiten der algebraischen Gleichungen
Methoden, mit denen man das bei hybriden dynamischen Systemen auftretende diskrete Verhalten implementieren kann
Glättung, Überwachung des Schaltzeitpunktes
implizite und explizite Transitionen bei hybriden Automaten
- Explizite Transitionen sind Funktionen der Zeit (und/)oder der Eingangsgrößen
- Implizite Transitionen sind Zustandfunktionen
Erklären Sie, wie man ohne mathematische Rechnung feststellen kann, ob ein DA-System einen Index größer 1 hat.
Sind die algebraischen Gleichungen eines DA-Systems nicht nach den algebraischen Variablen auflösbar, dann hat das System einen differentiellen Index größer Eins (Inzidenzmatrix der algebraischen Gleichungen hat nicht vollen Rang).
Shannon-Theorem
besagt, dass die Frequenz, mit der ein Signal abgetastet werden muss, mehr als doppelt so hoch sein muss, wie die höchste im Signal enthaltene Frequenz
zeitdiskretes und zeitkontinuierliches System
In einem zeitdiskreten System ändern die Zustände nur zu bestimmten, diskreten Zeitpunkten ihre Werte. In einem zeitkontinuierlichen System hingegen ändern sie sich kontinuierlich.
Sprungbedingung (hybrider Automat)
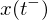 : bezeichnet den linksseitigen Grenzwert einer Variablen x am Zeitpunkt t, also den Wert vor dem Eintreten eines diskreten Ereignisses bei t
: bezeichnet den linksseitigen Grenzwert einer Variablen x am Zeitpunkt t, also den Wert vor dem Eintreten eines diskreten Ereignisses bei t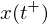 : bezeichnet den rechtsseitigen Grenzwert von x am Zeitpunkt t, also den Wert nach dem Eintreten eines diskreten Ereignisses
: bezeichnet den rechtsseitigen Grenzwert von x am Zeitpunkt t, also den Wert nach dem Eintreten eines diskreten EreignissesHybrider Automat
- Möglichkeit zur Modellierung hybrider Systeme
- hybride Systeme bestehen aus einem diskreten und einem kontinuierlichen Teil
- in Moden wird eine Differentialgleichung eingebettet, die kontinuierlichen Regler repräsentiert
- Übergang zwischen Moden ist diskret
Beispiel: elektrischer Schaltkreis
weist fast immer einen kontinuierlichen Verlauf von Strom und Spannung auf, wird aber zu diskreten Zeitpunkten durch schaltende Bauelemente (z.B. Transistoren) beeinflusst
Speichergrößen
differentielle Größen (speichern somit auch extensive Größen)
Bsp.: Position und Geschwindigkeit bei mechanischen Modellen
Bsp.: Position und Geschwindigkeit bei mechanischen Modellen
Matrizen A , B , C und D in der linearen Zustandsraumdarstellung
A: Systemmatrix
B: Eingangsmatrix
C: Ausgangsmatrix
D: Durchgangsmatrix
B: Eingangsmatrix
C: Ausgangsmatrix
D: Durchgangsmatrix
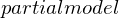 und
und 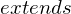 in Modelica
in Modelica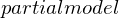 : unvollständiges Modelica-Modell, welches nicht alleine ausgeführt werden kann
: unvollständiges Modelica-Modell, welches nicht alleine ausgeführt werden kann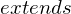 : Befehl, mit dem in einem Modelica-Modell die Variablen und Gleichungen eines unvollständigen Modells übernommen (geerbt) werden
: Befehl, mit dem in einem Modelica-Modell die Variablen und Gleichungen eines unvollständigen Modells übernommen (geerbt) werden Speicher- und Verknüpfungssysteme
Verknüpfungssysteme haben keine Zustände/ speichern keine
Masse, Stoffmenge, Energie o.a. extensive Größen.
Masse, Stoffmenge, Energie o.a. extensive Größen.
- Speichersystem: Kondensator, Spule
- Verknüpfungssystem: widerstandsloser Leiter
Warum ist eine Indexanalyse sinnvoll?
- Auswahl geeigneter numerischer Methoden (viele Simulatoren können nur Index-1)
- Bestimmung der Anzahl unabhängig zu spezifizierender Anfangsbedingungen
- Identifikation von algebraischen Zwangsbedingungen
Unterschied AVT - CATS
AVT: Es werden ausschließlich konzentrierte Systeme betrachtet
CATS: beschäftigt sich mit verteilten Systemen
CATS: beschäftigt sich mit verteilten Systemen
Zustandsraumkonzept
- geeignet für die Simulation und Analyse des dynamische Verhaltens von Systemen
- ermöglicht eine einheitliche und übersichtliche Veranschaulichung des Prozesses
- viele Softwaretools arbeiten mit Zustandsdarstellungen
- System von Differentialgleichungen, Vektorraum
Stabilität
für Startwerte innerhalb der δ-Umgebung der Ruhelage 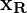 bleibt die Lösung des Systems immer in der
bleibt die Lösung des Systems immer in der  -Umgebung, überschreitet also nie den äußeren Kreis
-Umgebung, überschreitet also nie den äußeren Kreis

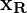 bleibt die Lösung des Systems immer in der
bleibt die Lösung des Systems immer in der  -Umgebung, überschreitet also nie den äußeren Kreis
-Umgebung, überschreitet also nie den äußeren Kreis 
Trajektorie
Für wachsende t beschreibt x(t) die Bahnkurve bzw. eine so genannte Trajektorie.
Phasenporträt: Trajektorien eines Systems für mehrere Anfangswerte im selben Diagramm
- dürfen Schlangenlinien fahren
- dürfen sich für verschiedene Anfangswerte nicht schneiden
- keine Sprünge, kein Knick
Phasenporträt: Trajektorien eines Systems für mehrere Anfangswerte im selben Diagramm
Stabilität linearer autonomer Systeme
stabil: Realteil der EW < 0
instabil: Realteil der EW > 0
grenzstabil: Realteil eines EW = 0, sonst <0
instabil: Realteil der EW > 0
grenzstabil: Realteil eines EW = 0, sonst <0
Berechnung Stabilität eines Systems
- Experimentell
- Direkte Stabilitätsanalyse nach Ljapunow
- Indirekte Stabilitätsanalyse nach Ljapunow
Indirekte Methode von Ljapunow
- Linearisierung um die Ruhelage
- es kann von den Realteilen der Eigenwerte auf das lokale Stabilitätsverhalten geschlossen werden
- Hartman-Grobman: Rückschluss vom linearisierten System auf das nichtlineare System ist nur zulässig, wenn die Matrix A keinen Eigenwert hat, dessen Realteil Null ist
Direkte Methode von Ljapunow
- erfolgt mit Hilfe der sogenannten Ljapunow-Funktion
- lässt sich direkt auf nichtlineare Systeme anwenden
Voraussetzungen:
1.
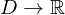
2.
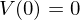
3. Definitheit: ist die Funktion indefinit, ist diese als Ljapunow Funktion ungeeignet (
 und
und 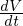 muss definit sein auf
muss definit sein auf 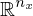 )
)Sensitivitätsmatrix
der Ausgänge 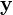 (Sensitivitätsmatrix der Zustände
(Sensitivitätsmatrix der Zustände 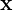 analog):
analog):

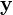 (Sensitivitätsmatrix der Zustände
(Sensitivitätsmatrix der Zustände 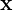 analog):
analog):
- zur Berechnung der Sensivitäten
- Zeilen m: Anzahl an Ausgängen/ Zuständen, Spalten n: Anzahl an Parametern (unterschiedliche Anzahl von von Parametern und Ausgängen möglich)
Grenzzyklus und Attraktor
- Wenn für beliebige Startwerte (außer der instabilen Ruhelage) alle Trajektorien auf eine geschlossene Trajektorie zulaufen, ist diese der Grenzzyklus und in diesem Fall der Attraktor
- Attraktor: eine Untermenge des Zustandsraums, der sich Systemzustände in einem bestimmten Einzugsbereich annähern und die unter der Dynamik des nichtlinearen Systems nicht mehr verlassen wird
- Ruhelagen sind Spezialfälle von Attraktoren
Einzugsbereich
Für stabile Ruhelage wird die Menge aller Punkte 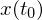 des Zustandsraums als Einzugsbereich bezeichnet, aus denen die Trajektorien x(t) für t → ∞ gegen die Ruhelage streben
des Zustandsraums als Einzugsbereich bezeichnet, aus denen die Trajektorien x(t) für t → ∞ gegen die Ruhelage streben
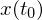 des Zustandsraums als Einzugsbereich bezeichnet, aus denen die Trajektorien x(t) für t → ∞ gegen die Ruhelage streben
des Zustandsraums als Einzugsbereich bezeichnet, aus denen die Trajektorien x(t) für t → ∞ gegen die Ruhelage strebenWie kann das Systemverhalten dargestellt werden?
- Zustand als explizite Funktion der Zeit auftragen
- Darstellung im Zustandsraum
Differentieller Index
- Ein Index von Null bezeichnet ein gewöhnliches Differentialgleichungssystem (DGL)
- Ein System in Zustandsdarstellung nach hat den Index 1
- Ein DA-System hat den Index größer oder gleich 1
Endlicher Automat
- Knoten beschreiben direkt die diskreten Zustände
- Übergänge zwischen diesen Zuständen werden durch gerichtete Kanten beschrieben
Kartensatzinfo:
Autor: CoboCards-User
Oberthema: Simulationstechnik RWTH
Thema: AVT
Veröffentlicht: 25.05.2018
Schlagwörter Karten:
Alle Karten (82)
keine Schlagwörter