Was sind „Syntax“ und „Semantik“ im Rahmen der Aussagelogik?
Die Syntax gibt hierbei an, wie formal korrekte Formeln gebildet werden können. Sie ist also vergleichbar mit der Grammatik einer Sprache, und sagt damit nichts über die inhaltliche Bedeutung der Sätze aus.
Die Semantik dahingegen geht auf die inhaltliche Bedeutung syntaktisch korrekter Strukturen ein. Im Rahmen der Aussagenlogik bezieht sich diese Interpretation jedoch nur auf die Bewertung
von Aussagen als „wahr“ oder „falsch“ aufgrund festgelegter Gesetzmäßigkeiten, der eigentliche Sinn der Elementaraussagen wird dabei nicht hinterfragt.
Die Semantik dahingegen geht auf die inhaltliche Bedeutung syntaktisch korrekter Strukturen ein. Im Rahmen der Aussagenlogik bezieht sich diese Interpretation jedoch nur auf die Bewertung
von Aussagen als „wahr“ oder „falsch“ aufgrund festgelegter Gesetzmäßigkeiten, der eigentliche Sinn der Elementaraussagen wird dabei nicht hinterfragt.
Was sind Normalformen? Was zeichnet die zwei verschiedenen Varianten aus?
Eindeutige Darstellung von Wahrheitsformeln. Sie dienen der Vergleichbarkeit.
Konjunktive Normalform: Konjunktive Verbindung von Disjunktionstermen

Disjunktive Normalform: DisjunktiveVerbindung von Konjunktionstermen

Konjunktive Normalform: Konjunktive Verbindung von Disjunktionstermen

Disjunktive Normalform: DisjunktiveVerbindung von Konjunktionstermen

Wie lautet der Algorithmus zur Erzeugung einer kDN / kKN?
1. Ausgehend von einer DN oder KN des Terms A suchen wir alle Terme, in welchen Variablen fehlen. Gibt es solche Terme nicht, liegt bereits eine kDN oder kKN vor und wir sind fertig.
2. Ansonsten wählen wir den ersten Konjunktionsterm K (Disjunktionsterm D) von A und eine Variable a, die nicht darin vorkommt.
3. Wir ersetzen K durch oder D durch
oder D durch  und können dann das Distributivgesetz anwenden.
und können dann das Distributivgesetz anwenden.
4. Wie schon beim Fall des Erzeugens der DN oder KN können gleiche Terme auftauchen, diese werden mit dem Idempotenzgesetz zusammengefasst.
2. Ansonsten wählen wir den ersten Konjunktionsterm K (Disjunktionsterm D) von A und eine Variable a, die nicht darin vorkommt.
3. Wir ersetzen K durch
 oder D durch
oder D durch  und können dann das Distributivgesetz anwenden.
und können dann das Distributivgesetz anwenden.4. Wie schon beim Fall des Erzeugens der DN oder KN können gleiche Terme auftauchen, diese werden mit dem Idempotenzgesetz zusammengefasst.
Wie werden Terme geordnet, um leichter eine Vergleichbarkeit herstellen zu können?
Wir übersetzen eine negierte Variable in eine „0“ und eine nichtnegierte Variable in eine „1“.
Hierdurch werden n-stellige Dualzahlen erzeugt, welche entsprechend ihrer Größe sortiert (links nach rechts: 000 bis 111). werden können und so die Position des entsprechenden Minterms oder Maxterms in der kDN oder kKN bestimmen.
Hierdurch werden n-stellige Dualzahlen erzeugt, welche entsprechend ihrer Größe sortiert (links nach rechts: 000 bis 111). werden können und so die Position des entsprechenden Minterms oder Maxterms in der kDN oder kKN bestimmen.
Was ist eine Boolesche Funktion?
Grundlage jeder Booleschen Funktion sind Variablen ai (i = 1, …, n), welchen eindeutig eine Belegung B  {0, 1} zugewiesen werden kann. Aus diesen werden syntaktisch korrekte Terme auf folgende Art und Weise gebildet:
{0, 1} zugewiesen werden kann. Aus diesen werden syntaktisch korrekte Terme auf folgende Art und Weise gebildet:
1. Jede Konstante 0 und 1 und jede Variable ai ist ein Boolescher Term.
2. Sind A und B Boolesche Terme, dann sind auch A’, (A B) und (A
B) und (A  B) Boolesche Terme.
B) Boolesche Terme.
3. Nur Zeichenreihen, die sich mit (1) und (2) in endlich vielen Schritten konstruieren lassen, sind Boolesche Terme.
 {0, 1} zugewiesen werden kann. Aus diesen werden syntaktisch korrekte Terme auf folgende Art und Weise gebildet:
{0, 1} zugewiesen werden kann. Aus diesen werden syntaktisch korrekte Terme auf folgende Art und Weise gebildet:1. Jede Konstante 0 und 1 und jede Variable ai ist ein Boolescher Term.
2. Sind A und B Boolesche Terme, dann sind auch A’, (A
 B) und (A
B) und (A  B) Boolesche Terme.
B) Boolesche Terme.3. Nur Zeichenreihen, die sich mit (1) und (2) in endlich vielen Schritten konstruieren lassen, sind Boolesche Terme.
Flashcard set info:
Author: learner94
Main topic: Mathematik
Topic: Logik & Algebra
Published: 26.08.2017
Card tags:
All cards (54)
no tags






 b
b
 b
b

 eine gültige Aussage? Was ist mit
eine gültige Aussage? Was ist mit  ?
? oder
oder  stehen darf.
stehen darf.










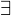 - es gibt mindestens ein Element
- es gibt mindestens ein Element - es existiert kein Element x
- es existiert kein Element x - für alle Elemente gilt
- für alle Elemente gilt


 M bedeutet, dass T Teilmenge der Menge M ist und die Mengen dabei nicht gleich sein dürfen.
M bedeutet, dass T Teilmenge der Menge M ist und die Mengen dabei nicht gleich sein dürfen.
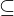 M ist kann umgekehrt gesagt werden, M ist eine Obermenge von T.
M ist kann umgekehrt gesagt werden, M ist eine Obermenge von T.  T wird somit gelesen als M ist Obermenge von T.
T wird somit gelesen als M ist Obermenge von T.






















