Topologie
Sei  eine Menge.
eine Menge.  ist ein Mengensystem und heißt Topologie auf
ist ein Mengensystem und heißt Topologie auf  falls gilt:
falls gilt:
(i)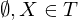 ,
,
(ii) Falls , so ist auch
, so ist auch  ,
,
(iii) Falls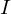 eine Indexmenge ist und
eine Indexmenge ist und  , so ist auch
, so ist auch 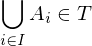 .
.
In diesem Fall heißt ein Topologischer Raum.
ein Topologischer Raum.
 eine Menge.
eine Menge.  ist ein Mengensystem und heißt Topologie auf
ist ein Mengensystem und heißt Topologie auf  falls gilt:
falls gilt:(i)
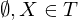 ,
,(ii) Falls
 , so ist auch
, so ist auch  ,
,(iii) Falls
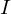 eine Indexmenge ist und
eine Indexmenge ist und  , so ist auch
, so ist auch 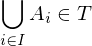 .
.In diesem Fall heißt
 ein Topologischer Raum.
ein Topologischer Raum.Beschränkte Abbildungen zwischen normierten Räumen
Seien 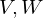 normierte Räume und
normierte Räume und  .
. 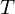 heißt beschränkt, falls es existiert ein
heißt beschränkt, falls es existiert ein  mit
mit  für alle
für alle  .
.
Bemerkung: Ist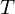 ein lineare Operator (eine lineare Abbildung) so gilt
ein lineare Operator (eine lineare Abbildung) so gilt 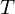 beschränkt
beschränkt 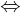
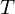 stetig.
stetig.
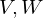 normierte Räume und
normierte Räume und  .
. 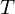 heißt beschränkt, falls es existiert ein
heißt beschränkt, falls es existiert ein  mit
mit  für alle
für alle  .
.Bemerkung: Ist
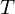 ein lineare Operator (eine lineare Abbildung) so gilt
ein lineare Operator (eine lineare Abbildung) so gilt 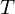 beschränkt
beschränkt 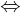
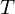 stetig.
stetig.Separabel
Ein normierter Raum heißt separabel, genau dann wenn es eine abzählbare linear unabhängige Menge 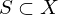 gibt, mit
gibt, mit  .
.
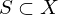 gibt, mit
gibt, mit  .
.Abzählbar
Ein Menge wird als abzählbar bezeichnet, wenn es eine Bijektion zwischen der Menge und den natürlichen Zahlen  existiert.
existiert.
 existiert.
existiert.Linear unabhängige Menge
Ein Menge  heißt linear unabhängig, falls es ex. kein
heißt linear unabhängig, falls es ex. kein 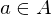 , welche lin. Komb. der anderen Vektoren in
, welche lin. Komb. der anderen Vektoren in  ist.
ist.
 heißt linear unabhängig, falls es ex. kein
heißt linear unabhängig, falls es ex. kein 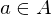 , welche lin. Komb. der anderen Vektoren in
, welche lin. Komb. der anderen Vektoren in  ist.
ist.Kartensatzinfo:
Autor: heinzwurst
Oberthema: Mathematik
Thema: Analysis
Schule / Uni: Universität Konstanz
Ort: Konstanz
Veröffentlicht: 03.05.2010
Schlagwörter Karten:
Alle Karten (6)
keine Schlagwörter



