Aussage und Aussageform=
2Punkte
2Punkte
eine Aussage ist ein Satz, der einen Sachverhalt beschreibt und entweder wahr oder falsch ist.
eine Aussageform ist ein Satz mit einer oder mehreren Variablen, wenn der Satz durch Einsetzen von Elementen geeigneter Grundmengen für die Variablen zu einer Aussage wird. Kann keinem Wahrheitswert zugeordnet werden. Eine Grundform ist stets vorzugeben.
eine Aussageform ist ein Satz mit einer oder mehreren Variablen, wenn der Satz durch Einsetzen von Elementen geeigneter Grundmengen für die Variablen zu einer Aussage wird. Kann keinem Wahrheitswert zugeordnet werden. Eine Grundform ist stets vorzugeben.
Erfüllingmenge (Lösungsmenge) und seine Gültigkeit=
2Punkte
2Punkte
gegeben ist eine Aussageform mit der Grundmenge G. Ein Element der Grundmenge G erfüllt die Aussageform, wenn seine Einsetzung zur einer wahren Aussage führt. Die Menge aller Elemente, die die Aussageform erfüllen, heißt Erfüllungsmenge der Aussageform.
Beispiel: p(x): x<3 Grundmenge: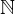
E =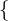 0, 1, 2
0, 1, 2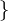
Aussageform heißt erfüllbar in G, wenn: E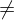
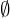
Aussageform heißt allgemeingültig in G, wenn: E=G
Aussageform heißt teilgültig in g, wenn: E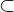 G
G
Beispiel: p(x): x<3 Grundmenge:
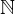
E =
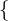 0, 1, 2
0, 1, 2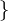
Aussageform heißt erfüllbar in G, wenn: E
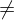
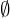
Aussageform heißt allgemeingültig in G, wenn: E=G
Aussageform heißt teilgültig in g, wenn: E
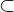 G
GImplikation=
Sind p(x) und q(x) beliebige Aussageformen in einer Grundmenge G, dann wird die Aussage p(x) 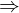 q(x) Implikation genannt, wenn die Erfüllungsmenge von p(x) eine Teilmenge der Erfüllungsmenge von q(x) ist.
q(x) Implikation genannt, wenn die Erfüllungsmenge von p(x) eine Teilmenge der Erfüllungsmenge von q(x) ist.
Beispiel: p(x): x<1 G =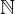 E = A
E = A
q(x): x<2 G =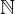 E = B
E = B
E von p(x): A =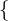 1
1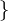
E von q(x): B =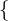 1,2
1,2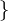
Zwischen den beiden Mengen besteht eine
Teilmengenbeziehung A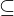 B
B
also ist auch p(x)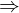 q(x)
q(x)
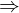 q(x) Implikation genannt, wenn die Erfüllungsmenge von p(x) eine Teilmenge der Erfüllungsmenge von q(x) ist.
q(x) Implikation genannt, wenn die Erfüllungsmenge von p(x) eine Teilmenge der Erfüllungsmenge von q(x) ist.Beispiel: p(x): x<1 G =
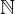 E = A
E = Aq(x): x<2 G =
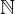 E = B
E = BE von p(x): A =
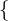 1
1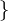
E von q(x): B =
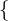 1,2
1,2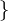
Zwischen den beiden Mengen besteht eine
Teilmengenbeziehung A
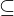 B
Balso ist auch p(x)
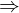 q(x)
q(x)Vorbereich und Nachbereich=
die Menge aller Elemente von A, denen mindestens ein Element von B zugeordnet wird, nennt man den Vorbereich der Relation R und bezeichnet ihn mit V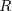
die Menge aller Elemente von B, die mindestens einem Element von A zugeordnet sind, nennt man den Nachbereich der Relation R und bezeichnet ihn mit N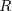
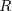
die Menge aller Elemente von B, die mindestens einem Element von A zugeordnet sind, nennt man den Nachbereich der Relation R und bezeichnet ihn mit N
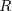
Flashcard set info:
Author: rosa11182
Main topic: Mathematik
Topic: Algebra
Published: 28.07.2010
Card tags:
All cards (22)
no tags



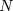
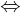 q(x) Äquivalenz genannt, wenn die Erfüllungsmenge von p(x) gleich der Erfüllungsmenge von q(x) ist.
q(x) Äquivalenz genannt, wenn die Erfüllungsmenge von p(x) gleich der Erfüllungsmenge von q(x) ist. gelesen?
gelesen? A und y
A und y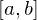
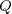 =
= 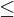 x
x 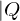
 mx+n, mit m, n
mx+n, mit m, n  ...
...