Wann ist ein lineares Gleichungssystem (LGS) konsistent?
Wenn alle 0 Zeilen der gegaussten Matrix = 0 sind (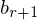 bis
bis 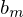 = 0)
= 0)
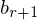 bis
bis 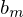 = 0)
= 0)Wann hat ein lineares Gleichungssystem mindestens eine Lösung?
- r = m
- r < m & konsistent
Wann hat ein lineares Gleichungssystem unendlich Lösungen?
n - r > 0  r < n & konsistent
r < n & konsistent
 r < n & konsistent
r < n & konsistentWann hat ein LGS für alle 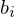 eine Lösung?
eine Lösung?
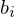 eine Lösung?
eine Lösung?Wenn A eine quadratische Matrix ist die für Ax = 0 nur die triviale Lösung gibt.
Welche Bedingungen in der Dimension der Matrix müssen erfüllt sein, damit eine Multiplikation möglich ist?
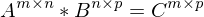
Eigenschaften invertierbarer (regulärer) Matrixen
-
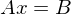 ist
ist 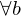 lösbar
lösbar -
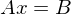 hat genau eine Lösung
hat genau eine Lösung -
 hat nur die triviale Lösung
hat nur die triviale Lösung -

-
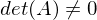
Eigenschaften nicht-invertierbarer (singulärer) Matrixen
-
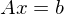 hat entweder keine oder unendlich viele Lösungen
hat entweder keine oder unendlich viele Lösungen -
 hat unendlich viele Lösungen
hat unendlich viele Lösungen -

-
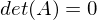
Eigenschaften einer orthogonalen Matrix
-

- A ist invertierbar &
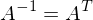
-
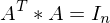
-
 : C ist auch orthogonal wenn A und B orthogonal
: C ist auch orthogonal wenn A und B orthogonal - Spalten und Zeilenvektoren sind normiert (
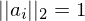 )
) - Spaltenvektoren sind im rechten Winkel aufeinander
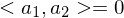
Welche Eigenschaften benötigt eine Matrix, damit man ihre Determinante finden kann?
Sie muss quadratisch sein
Was passiert mit der Determinante wenn eine Zeile vertauscht wird?
Sie wechselt das Vorzeichen
Was passiert bei der Addition eines vielfaches einer Zeile zur anderen mit der Determinante?
Sie bleibt unverändert
Was gilt für die Determinante wenn eine ganze Zeile skalar multipliziert wird?
Man kann den Skalar aus der Matrix nehmen und ihn mit der Determinante der Matrix ohne skalaren Faktor multiplizieren und kommt auf das selbe Resultat.
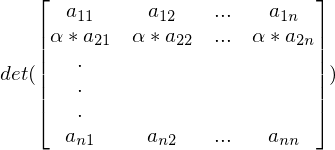
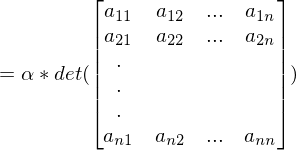
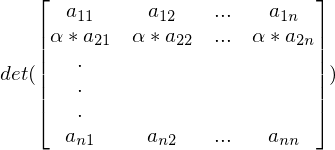
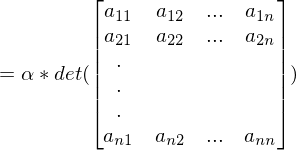
Bei welchen Matrizen ist die Determinante eine Multiplikation der Werte ihrer Diagonalen?
Bei einer L, R und diagonal Matrix
Was stellt die Determinante einer 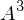 Matrix dar?
Matrix dar?
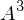 Matrix dar?
Matrix dar?Das Volumen das von 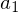 ,
, 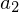 und
und 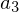 aufgespannt wird (
aufgespannt wird (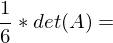 Pyramidenvolumen)
Pyramidenvolumen)
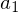 ,
, 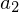 und
und 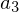 aufgespannt wird (
aufgespannt wird (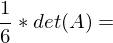 Pyramidenvolumen)
Pyramidenvolumen)Was ist ein endlich dimensionaler Raum?
Wenn ein Erzeugendensystem mit endlich vielen Vektoren gebildet werden kann.
Welche Eigenschaften hat ein Raum V mit dim(V) = n
- Mehr als n Vektoren sind linear Abhängig
- Weniger als n Vektoren sind nicht erzeugend
- n linear unabhängige Vektoren bilden eine Basis
Eigenschaften von Ker(A) und Im(A) 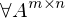
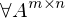
-
 ist ein lösbares LGS
ist ein lösbares LGS -
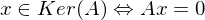
- Ker(A) ist ein Unterraum von

- Im(A) ist ein Unterraum von
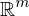
- Es gilt
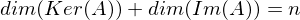
- Es gilt

Wie bekommt man die Basis des Ker(A)?
Man setzt Ax = 0 und gausst, span vom x Vektor ergibt die Basis des Ker(A)
Wie bekommt man die Basis des Im(A)
Man nimmt linear unabhängige Vektoren in A. (Wenn zuerst der Ker(A) bestimmt wurde können diese gleich abgelesen werden)
Was ist eine Eigenschaft der EW zu 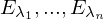 wenn die EV linear unabhängig sind?
wenn die EV linear unabhängig sind?
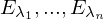 wenn die EV linear unabhängig sind?
wenn die EV linear unabhängig sind?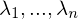 sind paarweise verschieden
sind paarweise verschiedenWas sind Gemeinsamkeiten von zwei ähnlichen Matrizen?
Charakteristisches Polynom, EW und algebraische Vielfachheit
Wann ist eine Matrix halbeinfach?
Wenn bei jedem EW, EV paar, die algebraische Vielfachheit gleich der gemetrischen Vielfachheit ist.
Wie wird T und D gebildet?
T sind die EV von A
D sind die EW von A auf der Diagonale eingetragen.
D sind die EW von A auf der Diagonale eingetragen.
Eigenschaften der EW symmetrischer Matrizen
- Alle EW von
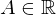
- EV von verschiedenen EW sind orthogonal
- A ist halbeinfach (also auch diagonalisierbar)
- Mit normierten Spalten von T kann die Orthonormalbasis von T gebildet werden
Axiome der Matrixnorm
-
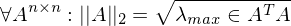
-
 orthogonale
orthogonale 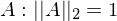
-
 symmetrische
symmetrische 
-
 reguläre
reguläre 
-
 reguläre & symmetrische
reguläre & symmetrische 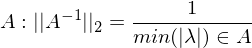
-
 max Spaltensummennorm = Addition des Betrags der Einträge der Spalte
max Spaltensummennorm = Addition des Betrags der Einträge der Spalte -
 max Zeilensummennorm = Addition des Betrages der Einträge der Zeile
max Zeilensummennorm = Addition des Betrages der Einträge der Zeile
Was ist das Hurwitz Kriterium?
Es sagt, dass jede Matrix positiv definit ist wenn die Determinante alle ihrer quadratischen Untermatrixen strikt grösser Null ist.
Wie erreicht man das Ziel der Ausgleichsrechnung und was soll erreicht werden?
Man will 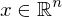 so finden, das
so finden, das 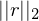 minimal wird.
minimal wird.
Und es gilt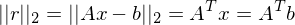
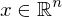 so finden, das
so finden, das 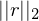 minimal wird.
minimal wird.Und es gilt
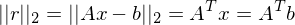
Was sind die Schritte der LR-Zerlegung für 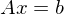 ?
?
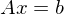 ?
?- Die Matrix A wird in L und R Zerlegt durch Gaussen (ausschliesslich mit Subtraktion) der Matrix A (P Matrix nicht vergessen)
- Danach gilt
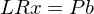
-
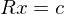 wird zu c zusammengeführt
wird zu c zusammengeführt - Das führt zu
 wo nun nach c aufgelöst werden kann
wo nun nach c aufgelöst werden kann - Mit gefundenem c kann nun für x aufgelöst werden über

Was sind die Schritte der QR-Zerlegung für 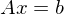 ?
?
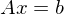 ?
?- Die Matrix A wird in Q Zerlegt durch eine Serie von Givensrotationen mit der A Matrix
- Danach gilt

- Dann soll auf R geschlossen werden mit

- Mit gefundenem R kann nun für x aufgelöst werden über

Was sind die Schritte des Gramm-Schmidt Orthogonalisierungsverfahren?
1. Etablierung des ersten Basisvektors: 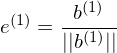
2. Errechnung der Richtung des zweiten Basisvektors:
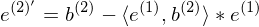
3. Normalisierung des zweiten Basisvektors: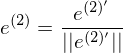
4. Repetition von Schritt 2. und 3. für alle weiter Vektoren der originalen Basis.
Schritt 2. ist jeweils im Schema:
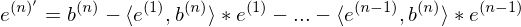
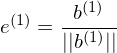
2. Errechnung der Richtung des zweiten Basisvektors:
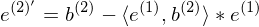
3. Normalisierung des zweiten Basisvektors:
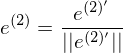
4. Repetition von Schritt 2. und 3. für alle weiter Vektoren der originalen Basis.
Schritt 2. ist jeweils im Schema:
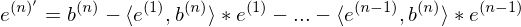
Was ist eine Übergangsmatrix?
Eine Matrix die verwendet wird um von einer Basis in die nächste zu wechseln.
Wie schliesst man auf eine Übergangsmatrix T die von 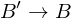 geht?
geht?
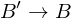 geht?
geht?Man stellt die Basisvektoren von der alten Basis (B') in der neuen dar (B).
Mit den Multiplikationswerten kann eine Matrix gebildet werden, welche wenn sie transponiert wird T ergibt.
Bsp:
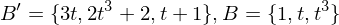
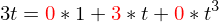
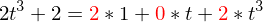
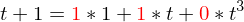
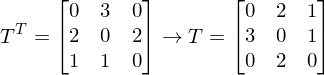
Mit den Multiplikationswerten kann eine Matrix gebildet werden, welche wenn sie transponiert wird T ergibt.
Bsp:
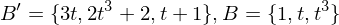
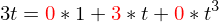
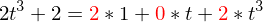
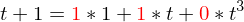
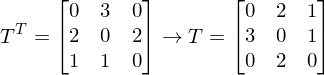
Wie kann die Darstellungsmatrix 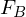 zur Matrix
zur Matrix 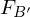 konvertiert werden mit der Übergangsmatrix
konvertiert werden mit der Übergangsmatrix 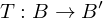
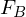 zur Matrix
zur Matrix 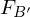 konvertiert werden mit der Übergangsmatrix
konvertiert werden mit der Übergangsmatrix 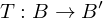
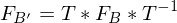
Wie wird 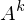 berechnet für A quadratisch und diag-bar?
berechnet für A quadratisch und diag-bar?
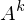 berechnet für A quadratisch und diag-bar?
berechnet für A quadratisch und diag-bar?1. EWP von A lösen
2. T und D bilden
3. Schauen ob A symmetrisch
Nein: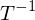 berechnen
berechnen 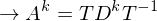
Ja: T orthogonal wählen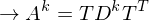
2. T und D bilden
3. Schauen ob A symmetrisch
Nein:
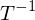 berechnen
berechnen 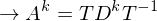
Ja: T orthogonal wählen
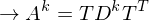
Eigenschaften positiver definitheit
-

- Matrix ist nicht singulär und es existiert eine inerse
- Alle Hauptelement der Diagonalen sind positiv
Was wird die Ausgleichsrechnung mit einer QR Zerlegung für die Matrix 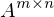 ausgeführt?
ausgeführt?
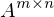 ausgeführt?
ausgeführt?1. Q Matrix bilden
2. R bilden: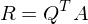
3.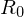 aus R extrahieren:
aus R extrahieren: 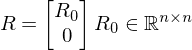
4. d bilden: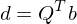
5.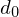 aus d extrahieren:
aus d extrahieren: 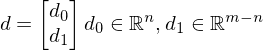
6. Nach x auflösen: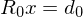
2. R bilden:
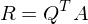
3.
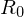 aus R extrahieren:
aus R extrahieren: 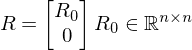
4. d bilden:
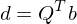
5.
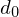 aus d extrahieren:
aus d extrahieren: 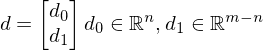
6. Nach x auflösen:
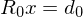
Was ist eine unitäre Matrix?
Eine komplexe Matrix die orthogonal bezüglich des Standartskalarproduktes ist.
Was ist eine Eigenschaft der U und V Matrix der Singulärwertzerlegung?
Sie sind orthogonal
Wie wird die V Matrix der Singulärwertzerlegung errechnet werden?
- Lösen des EWP von
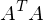
- V ist die Matrix bestehend aus den EV.
- Die Reihenfolge der Matrix korrespondiert zu ihren entsprechenden EW wenn diese vom grössten zum kleinsten geordnet werden.
- V wird orthonormalisiert (mit Gramm-Schmidt)
Wie wird die U Matrix der Singulärwertzerlegung errechnet werden?
- Lösen des EWP von
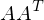
- U ist die Matrix bestehend aus den EV.
- Die Reihenfolge der Matrix korrespondiert zu ihren entsprechenden EW wenn diese vom grössten zum kleinsten geordnet werden.
- U wird orthonormalisiert (mit Gramm-Schmidt)
Wie wird die S Matrix einer 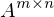 Matrix mit der Singulärwertzerlegung gebildet?
Matrix mit der Singulärwertzerlegung gebildet?
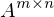 Matrix mit der Singulärwertzerlegung gebildet?
Matrix mit der Singulärwertzerlegung gebildet?Die Singulärwerte 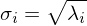 werden vom grössten zum kleinsten auf der Diagonalachse einer
werden vom grössten zum kleinsten auf der Diagonalachse einer 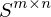 Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
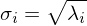 werden vom grössten zum kleinsten auf der Diagonalachse einer
werden vom grössten zum kleinsten auf der Diagonalachse einer 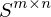 Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
Matrix eingetragen. Alle anderen Werte werden 0 gelassen.Von welcher Matrix muss das EWP gelöst werden um auf die U Matrix zu schliessen bei der SWP?
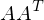
Von welcher Matrix muss das EWP gelöst werden um auf die V Matrix zu schliessen bei der SWP?
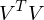
Wie kann die 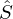 Matrix einer
Matrix einer 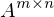 Matrix mit der Singulärwertzerlegung gebildet werden?
Matrix mit der Singulärwertzerlegung gebildet werden?
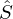 Matrix einer
Matrix einer 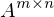 Matrix mit der Singulärwertzerlegung gebildet werden?
Matrix mit der Singulärwertzerlegung gebildet werden?Die Singulärwerte 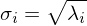 werden vom grössten zum kleinsten auf der Diagonalachse einer
werden vom grössten zum kleinsten auf der Diagonalachse einer 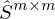 Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
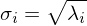 werden vom grössten zum kleinsten auf der Diagonalachse einer
werden vom grössten zum kleinsten auf der Diagonalachse einer 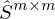 Matrix eingetragen. Alle anderen Werte werden 0 gelassen.
Matrix eingetragen. Alle anderen Werte werden 0 gelassen.Wie kann die Matrix 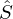 aus der S Matrix herausgelesen werden?
aus der S Matrix herausgelesen werden?
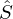 aus der S Matrix herausgelesen werden?
aus der S Matrix herausgelesen werden?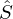 entspricht der in S vorkommenden quadratischen Diagonalmatrix.
entspricht der in S vorkommenden quadratischen Diagonalmatrix.Wie kann von der V Matrix auf die U Matrix geschlossen werden?
Es wird 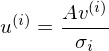 für jeden Vektor in V gerechnet.
für jeden Vektor in V gerechnet.
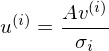 für jeden Vektor in V gerechnet.
für jeden Vektor in V gerechnet.Wie kann von der U Matrix auf die V Matrix geschlossen werden?
Es wird 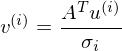 für jeden Vektor in U gerechnet.
für jeden Vektor in U gerechnet.
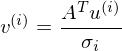 für jeden Vektor in U gerechnet.
für jeden Vektor in U gerechnet.Wie ist der Vektor d der Singulärwertzerlegung aufgeteilt?
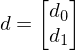 wobei
wobei  hat die selbe Dimension wie ein Vektor von
hat die selbe Dimension wie ein Vektor von 
Wie wird der Vektor v für die Haushodertransformation gewählt?
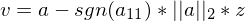
- z ist der Zielvektor, also z.B. ein Einheitsvektor
- a ist der Ausgangsvektor, also der zu spiegelnde Vektor
-
 ist der Eintrag der im der oberen linken Ecke auf die die H Matrix angewendet wird
ist der Eintrag der im der oberen linken Ecke auf die die H Matrix angewendet wird
Wie wird die Givensrotationsmatrix gewählt wenn der Eintrag 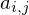 der Matrix
der Matrix 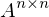 zu Null gemacht werden soll?
zu Null gemacht werden soll?
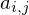 der Matrix
der Matrix 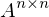 zu Null gemacht werden soll?
zu Null gemacht werden soll?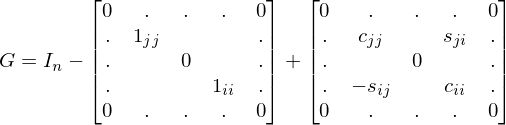
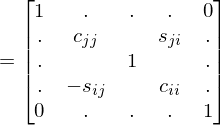
Wie löst man das DLG 1. Ordnung 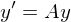 für A diag bar?
für A diag bar?
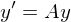 für A diag bar?
für A diag bar?1. Man löst das EWP für A und erstellt D von a und T von A
2. Man setzt die Werte in die Gleichung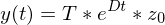
(für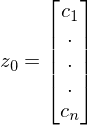
Also erhält man:
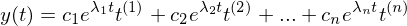
2. Man setzt die Werte in die Gleichung
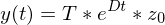
(für
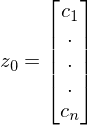
Also erhält man:
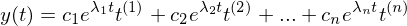
Kartensatzinfo:
Autor: CoboCards-User
Oberthema: Lineare Algebra I
Thema: Lineare Algebra
Schule / Uni: ETH Zürich
Ort: Zürich
Veröffentlicht: 21.01.2020
Tags: 2019
Schlagwörter Karten:
Alle Karten (188)
keine Schlagwörter






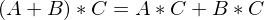

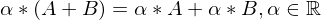

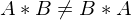


















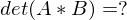




 und n ungerade?
und n ungerade?
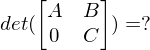

 Matrix dar?
Matrix dar?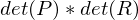
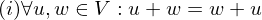
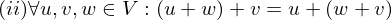





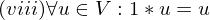

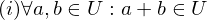

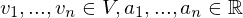 ist gleich
ist gleich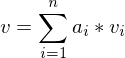

 lösbar
lösbar

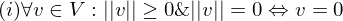


 = länge Vektor
= länge Vektor des grössten Eintrages in
des grössten Eintrages in 

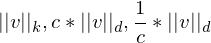 zu ordnen?
zu ordnen?

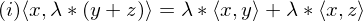

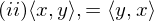
 (positive definitheit)
(positive definitheit)
 (gilt für jedes Skalarprodukt)
(gilt für jedes Skalarprodukt)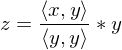



 (Pythagoras)
(Pythagoras)


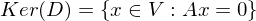
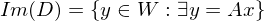

 wenn
wenn 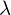 ein Eigenwert von
ein Eigenwert von  ist.
ist.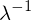
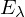 von A zu
von A zu  ?
? ähnlich?
ähnlich?


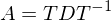

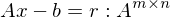 mit
mit 
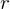
 ?
?
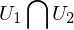
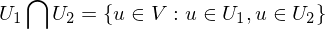
 wenn
wenn 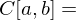 stetige Funktionen}?
stetige Funktionen}?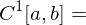 {1 mal diffbare stetige Funktionen}
{1 mal diffbare stetige Funktionen}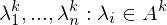
 berechnet werden wenn b gesucht ist?
berechnet werden wenn b gesucht ist? berechnen
berechnen berechnen
berechnen berechnen
berechnen mit einer Summe dargestellt?
mit einer Summe dargestellt?

 ?
?
 auch dargestellt werden?
auch dargestellt werden?
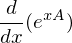 , wenn
, wenn 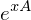 stetig diffbar?
stetig diffbar?

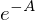
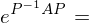
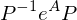
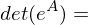









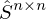




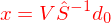


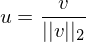
 gewählt wenn es aus einer
gewählt wenn es aus einer  Matrix stammt und angewendet wird
Matrix stammt und angewendet wird
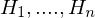 gefunden sind?
gefunden sind?

 gefunden sind?
gefunden sind?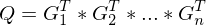
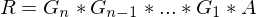



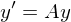
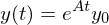
 auch geschrieben werden?
auch geschrieben werden?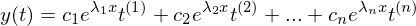
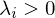

 bei einer symmetrischen positiv definiten Matrix A?
bei einer symmetrischen positiv definiten Matrix A?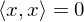 ?
?