Gleichheit von Vektoren
Zwei Vektoren sind dann genau gleich, wenn sie die durch ein und denselben Pfeil beschrieben werden können. Genau dann stimmen die zugehörigen Pfeilklassen überein.
Definition Vektor
Unter einem Vektor versteht man die Menge aller Pfeile, die gleich lang zueinander parallel und gleich orientiert sind. Ein einzelner Pfeil auf dieser Menge heißt Repräsentant des Vektors.
Ein Vektor ist ein Zahlentripel aus drei Koordinaten:
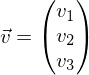
Ein Vektor ist ein Zahlentripel aus drei Koordinaten:
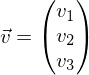
Addition zweier Vektoren
Dies bedeutet die Nacheinanderausführung der jeweiligen Verschiebungen.
Das Resultat lässt sich wieder als Vektor beschreiben.
Praxis: Addition der Koordinaten

Das Resultat lässt sich wieder als Vektor beschreiben.
Praxis: Addition der Koordinaten

Welche Gesetze gelten bei der Addition von Vektoren?
Kommutativgesetz a+b=b+a
Assoziativgesetz (a+b)+c= a+(b+c)
Assoziativgesetz (a+b)+c= a+(b+c)
Subtraktion zweier Vektoren
Man subtrahiert zwei Vektoren von einander, indem man den entgegensetzten Vektor zu dem anderen Vektor dazu addiert.
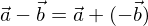
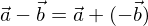
Nullvektor
Der Vektor, der jeden Punkt auf sich selbst abbildet.
Länge null
keine Richtung
Länge null
keine Richtung
Vervielfachung eines Vektors
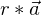
wenn r>0 Vektor gleichgerichtet
wenn r<0 Vektor ist entgegengesetzt gleichgerichtet
wenn r=0 -> Nullvektor
Betrag eines Vektors
 ist gleich der Strecke
ist gleich der Strecke 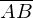
Wenn
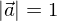 dann wird dieser als Einheitsvektor bezeichnet.
dann wird dieser als Einheitsvektor bezeichnet.
Für eine Strecke gilt:
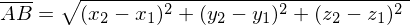
Parallelität eines Vektors
Eine Vektor 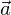 ist genau dann zu einem Vektor
ist genau dann zu einem Vektor 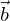 parallel, wenn es eine reelle Zahl r oder eine reelle Zahl s gibt, sodass gilt
parallel, wenn es eine reelle Zahl r oder eine reelle Zahl s gibt, sodass gilt
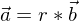 und
und 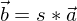
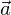 ist genau dann zu einem Vektor
ist genau dann zu einem Vektor 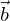 parallel, wenn es eine reelle Zahl r oder eine reelle Zahl s gibt, sodass gilt
parallel, wenn es eine reelle Zahl r oder eine reelle Zahl s gibt, sodass gilt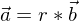 und
und 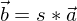
Linearkombination eines Vektors
Der Vektor 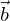 ist eine Linearkombination der Vektoren
ist eine Linearkombination der Vektoren 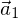 und
und  , wenn es reelle Zahlen
, wenn es reelle Zahlen 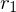 und
und 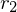 gibt, sodass
gibt, sodass 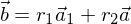 gilt.
gilt.
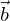 ist eine Linearkombination der Vektoren
ist eine Linearkombination der Vektoren 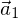 und
und  , wenn es reelle Zahlen
, wenn es reelle Zahlen 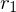 und
und 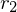 gibt, sodass
gibt, sodass 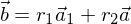 gilt.
gilt.Lineare Unabhängigkeit
Die Vektoren 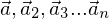 sind linear unabhängig, wenn sich kein Vektor von diesen als Linearkombination darstellen lässt.
sind linear unabhängig, wenn sich kein Vektor von diesen als Linearkombination darstellen lässt.
Lässt sich wenigstens ein Vektor der Vektoren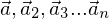 mit einer Linearkombination darstellen, so bezeichnet man die Vektoren linear abhängig.
mit einer Linearkombination darstellen, so bezeichnet man die Vektoren linear abhängig.
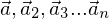 sind linear unabhängig, wenn sich kein Vektor von diesen als Linearkombination darstellen lässt.
sind linear unabhängig, wenn sich kein Vektor von diesen als Linearkombination darstellen lässt. Lässt sich wenigstens ein Vektor der Vektoren
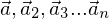 mit einer Linearkombination darstellen, so bezeichnet man die Vektoren linear abhängig.
mit einer Linearkombination darstellen, so bezeichnet man die Vektoren linear abhängig.Lineare Unabhängigkeit überprüfen
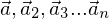 sind linear unbhängig, wenn aus
sind linear unbhängig, wenn aus 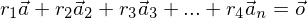 stets
stets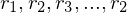 = 0 folgt.
= 0 folgt. Wenn allerdings nicht alle
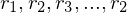 gleich null sind, dann sind
gleich null sind, dann sind 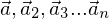 linear abhängig.
linear abhängig. Orthogonalität zwischen zwei Vektoren
Wenn zwei Vektoren senkrecht aufeinander stehen, so ist das Skalarprodukt = 0.
Geradengleichung
Die Gerade g, die durch den Punkt 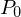 mit dem Stützvektor
mit dem Stützvektor 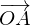 und dem Richtungsvektor
und dem Richtungsvektor  bestimmt ist, kann durch die Gleichung
bestimmt ist, kann durch die Gleichung 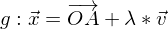 beschrieben werden.
beschrieben werden.
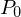 mit dem Stützvektor
mit dem Stützvektor 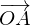 und dem Richtungsvektor
und dem Richtungsvektor  bestimmt ist, kann durch die Gleichung
bestimmt ist, kann durch die Gleichung 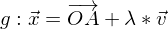 beschrieben werden.
beschrieben werden. Parallelität von Geraden
Zwei Geraden  und
und  der Ebene oder des Raumes sind genau dann parallel zueinander, wenn die zugehörigen Richtungsvektoren
der Ebene oder des Raumes sind genau dann parallel zueinander, wenn die zugehörigen Richtungsvektoren  und
und  linear abhängig (also parallel) sind.
linear abhängig (also parallel) sind.
 und
und  der Ebene oder des Raumes sind genau dann parallel zueinander, wenn die zugehörigen Richtungsvektoren
der Ebene oder des Raumes sind genau dann parallel zueinander, wenn die zugehörigen Richtungsvektoren  und
und  linear abhängig (also parallel) sind.
linear abhängig (also parallel) sind.Schnittwinkel zweier Geraden
- Berechnung mit Skalarprodukt
- Schnittwinkel muss zwischen
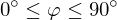 sein
sein
Gleichungssystem - zweier Geraden
keine Lösung: Parallelität überprüfen (lineare Abhängigkeit)-> falls nein ->  und
und  sind windschief
sind windschief
eine Lösung: es gibt einen Schnittpunkt S -> Spezialfall Orthogonaler Schnittpunkt
unendliche viele Lösungen: und
und  sind gleich
sind gleich
 und
und  sind windschief
sind windschiefeine Lösung: es gibt einen Schnittpunkt S -> Spezialfall Orthogonaler Schnittpunkt
unendliche viele Lösungen:
 und
und  sind gleich
sind gleichNormalenvektor
Einen zu den Spannvektoren  und
und  einer Ebene
einer Ebene  orthogonalen Vektor
orthogonalen Vektor 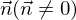 nennt man Normalenvektor von
nennt man Normalenvektor von  . Der zugehörige Einheitsvektor heißt Normaleneinheitsvektor und wird mit
. Der zugehörige Einheitsvektor heißt Normaleneinheitsvektor und wird mit  bezeichnet.
bezeichnet.
 und
und  einer Ebene
einer Ebene  orthogonalen Vektor
orthogonalen Vektor 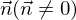 nennt man Normalenvektor von
nennt man Normalenvektor von  . Der zugehörige Einheitsvektor heißt Normaleneinheitsvektor und wird mit
. Der zugehörige Einheitsvektor heißt Normaleneinheitsvektor und wird mit  bezeichnet.
bezeichnet. Hesseche Normalenform der Gleichung einer Ebene im Raum
Eine Ebene  , die durch den Punkt
, die durch den Punkt 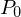 und ihren Normaleneinheitsvektor
und ihren Normaleneinheitsvektor  und den Normalenvektor
und den Normalenvektor 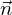 bestimmt ist, kann durch die Gleichung
bestimmt ist, kann durch die Gleichung 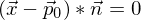 beschrieben werden.
beschrieben werden.
 , die durch den Punkt
, die durch den Punkt 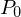 und ihren Normaleneinheitsvektor
und ihren Normaleneinheitsvektor  und den Normalenvektor
und den Normalenvektor 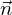 bestimmt ist, kann durch die Gleichung
bestimmt ist, kann durch die Gleichung 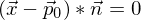 beschrieben werden.
beschrieben werden. Koordinatenform einer Ebene im Raum
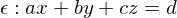
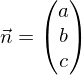
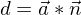 der
der  ist in diesem Fall der Stützvektor der Ebene.
ist in diesem Fall der Stützvektor der Ebene. Achsenabschnittsform einer Ebene
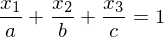
Beispiel:
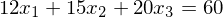

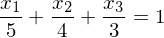
Jede Ebene in Koordinatenform lässt sich so schnell in die Achsenabschnittsform umwandeln.
Lagebeziehung Gerade - Ebene LGS
LGS
- hat genau eine Lösung -> g schneidet E in genau einem Punkt Richtungsvektoren
 von g ist unabhängig von den Richtungsvektoren der Ebene
von g ist unabhängig von den Richtungsvektoren der Ebene 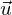 und
und 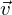
- hat keine Lösung -> g ist parallel zu E -> Richtungsvektoren von g und E sind linear abhängig
- hat unendlich viele Lösungen -> g liegt in E -> Richtungsvektoren von g und E sind linear abhängig
Schnittgerade von zwei Ebene händisch bestimmen
1. LGS aufstellen -> beide Ebenengleichungen gleichsetzen
2. einen beliebigen Parameter für eine Variable einführen
3. Gaußsches Eliminationsverfahren
4. Den Parameter für die Variable in die Ebenengleichung und eine weitere Lösung einsetzten
Beispiel
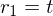

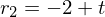
 Für
Für  wurde der Parameter t eingeführt
wurde der Parameter t eingeführt
Ebenengleichung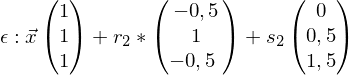
Für und
und 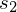 einsetzten
einsetzten
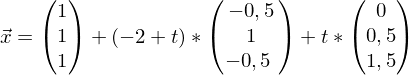
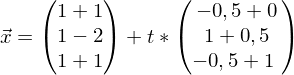
2. einen beliebigen Parameter für eine Variable einführen
3. Gaußsches Eliminationsverfahren
4. Den Parameter für die Variable in die Ebenengleichung und eine weitere Lösung einsetzten
Beispiel
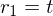

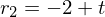
 Für
Für 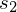 wurde der Parameter t eingeführt
wurde der Parameter t eingeführtEbenengleichung
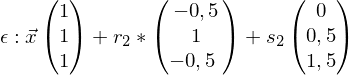
Für
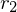 und
und 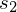 einsetzten
einsetzten 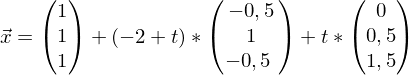
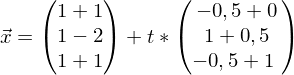
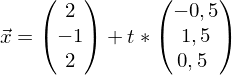
Schnittgerade von zwei Ebenen mit GTR bestimmen
1. LGS/ Matrix in GTR eingeben

2. 2nd Matrix - RREF([A]

3. Lösung aufstellen
Daraus folgt:
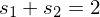
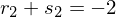

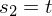 t wird als Parameter für
t wird als Parameter für 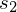 eingeführt
eingeführt
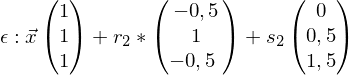
Für und
und 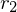 einsetzen
einsetzen
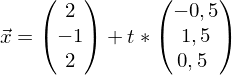

2. 2nd Matrix - RREF([A]

3. Lösung aufstellen
Daraus folgt:

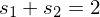
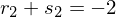

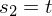 t wird als Parameter für
t wird als Parameter für 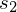 eingeführt
eingeführt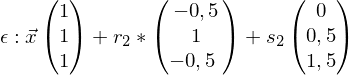
Für
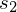 und
und 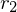 einsetzen
einsetzen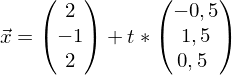
Schnittwinkel von zwei Ebenen
- Normalenvektoren der beiden Ebenen
- mithilfe des Skalarproduktes den Winkel ausrechnen
- Schnittwinkel muss zwischen
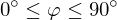 sein
sein
Schnittwinkel von Gerade und Ebene
- Normalenvektor von der Ebene
- Richtungsvektor der Gerade
- mithilfe des Skalarproduktes den Winkel
 ausrechnen
ausrechnen - von
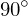 den Winkel
den Winkel  abziehen s. Skizze
abziehen s. Skizze - Schnittwinkel muss zwischen
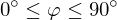 sein
sein

Abstand Ebene Punkt
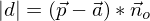 der Vektor
der Vektor  muss natürlich in der Stützvektor der Ebene sein
muss natürlich in der Stützvektor der Ebene sein
Beispiel:
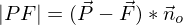

Abstand Ebene Gerade
- funktioniert nur bei Parallelität
- Abstandsberechnung über hessesche Normalenform
- als "Abstandpunkt" kann man z.B. den Stützvektor wählen
Abstand Ebene - Ebene
- nur bei Parallelität
- möglicher "Abstandpunkt" Stütsvektor der anderen Ebene
Abstand Gerade - Gerade
- bei Parallelität kann man mit dem Stützvektor der anderen Gerade den Abstand berechnen -> wird zum "Abstandspunkt" der Geraden
Geraden windschief zu einander:
- zwei Ebenengleichungen aufstellen
- Richtungsvektoren der Ebene sind die Richtungsvektoren der zwei Gerade
- Stützvektor ist einmal der von
 und einmal von
und einmal von  *Abstand Ebene berechnen
*Abstand Ebene berechnen
Kartensatzinfo:
Autor: JamesBond007
Oberthema: Mathematik
Thema: Analytische Geometrie
Veröffentlicht: 07.11.2013
Schlagwörter Karten:
Alle Karten (36)
keine Schlagwörter



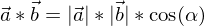 das Skalarprodukt
das Skalarprodukt


 sind linear abhängig
sind linear abhängig

