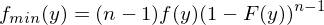Definition eines Wahrscheinlichkeitsraums (diskreter Fall) und der darin vorkommenden Größen!
Das Tupel  heißt Wahrscheinlichkeitsraum. Dabei bezeichnet
heißt Wahrscheinlichkeitsraum. Dabei bezeichnet  den Ereignisraum also die nichtleere Menge aller möglichen Versuchsergebnisse,
den Ereignisraum also die nichtleere Menge aller möglichen Versuchsergebnisse, 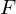 die Menge der Ereignisse
die Menge der Ereignisse  , die uns interessieren und
, die uns interessieren und 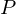 das Wahrscheinlichkeitsmaß, das jedem Ereignis aus
das Wahrscheinlichkeitsmaß, das jedem Ereignis aus 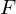 eine Wahrscheinlichkeit zuordnet.
eine Wahrscheinlichkeit zuordnet.
 heißt Wahrscheinlichkeitsraum. Dabei bezeichnet
heißt Wahrscheinlichkeitsraum. Dabei bezeichnet  den Ereignisraum also die nichtleere Menge aller möglichen Versuchsergebnisse,
den Ereignisraum also die nichtleere Menge aller möglichen Versuchsergebnisse, 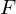 die Menge der Ereignisse
die Menge der Ereignisse  , die uns interessieren und
, die uns interessieren und 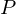 das Wahrscheinlichkeitsmaß, das jedem Ereignis aus
das Wahrscheinlichkeitsmaß, das jedem Ereignis aus 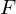 eine Wahrscheinlichkeit zuordnet.
eine Wahrscheinlichkeit zuordnet.(Stochastische) Unabhängigkeit zweier Ereignisse + Beziehung zw. stochastischer und paarweiser Unabhängigkeit bei mehr als 2 Ereignissen

Stochastische Unabhängigkeit ist die Unabhängigkeit jeder Teilfamilie der Ereignisse. Demnach folgt aus stochastischer Unabhängigkeit die paarweise Unabhängigkeit aber nicht umgekehrt!
Möglichkeiten der Auswahl von k aus n Elementen unter Berücksichtigung der Reihenfolge und ohne zurücklegen?

Möglichkeiten der Auswahl von k aus n verschiedenen Elementen ohne Reihenfolge und ohne Zurücklegen?

Formel für Stichproben des Umfangs n aus N untersch. Kugeln mit Zurücklegen in Reihenfolge?

Formel für Stichproben des Umfangs n aus N untersch. Kugeln
ohne Zurücklegen in Reihenfolge?
ohne Zurücklegen in Reihenfolge?

Formel für Stichproben des Umfangs n aus N untersch. Kugeln mit Zurücklegen ohne Reihenfolge?

Formel für Stichproben des Umfangs n aus N untersch. Kugeln ohne Zurücklegen ohne Reihenfolge?

Beliebiges Beispiel für einen Run
z.B.: 
 ist ein Audi Run der Länge 2, danach ein BMW Run der Länge 3 und schließlich ein Audi Run der Länge 1. Insgesamt sind es zwei Audi Runs und ein BMW Run.
ist ein Audi Run der Länge 2, danach ein BMW Run der Länge 3 und schließlich ein Audi Run der Länge 1. Insgesamt sind es zwei Audi Runs und ein BMW Run.

 ist ein Audi Run der Länge 2, danach ein BMW Run der Länge 3 und schließlich ein Audi Run der Länge 1. Insgesamt sind es zwei Audi Runs und ein BMW Run.
ist ein Audi Run der Länge 2, danach ein BMW Run der Länge 3 und schließlich ein Audi Run der Länge 1. Insgesamt sind es zwei Audi Runs und ein BMW Run.Definition einer Zufallsvariable  ?
?
 ?
?Ist  ein Wahrscheinlichkeitsraum und
ein Wahrscheinlichkeitsraum und  eine beliebige Menge, dann heißt
eine beliebige Menge, dann heißt  eine
eine  -wertige Zufallsvariable. Hierbei ordnet
-wertige Zufallsvariable. Hierbei ordnet  einem zufällig gewähltem
einem zufällig gewähltem 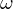 einen Wert
einen Wert  zu.
zu.
 ein Wahrscheinlichkeitsraum und
ein Wahrscheinlichkeitsraum und  eine beliebige Menge, dann heißt
eine beliebige Menge, dann heißt  eine
eine  -wertige Zufallsvariable. Hierbei ordnet
-wertige Zufallsvariable. Hierbei ordnet  einem zufällig gewähltem
einem zufällig gewähltem 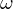 einen Wert
einen Wert  zu.
zu.Definition des Erwartungswerts einer reellwertigen Zufallsvariable 

Der Erwartungswert ist definiert als  , falls
, falls  existiert
existiert
 , falls
, falls  existiert
existiertWas ist eine Hypergeometrische Verteilung?
Seien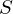 schwarze und
schwarze und  andere Kugeln in einer Urne, was ist
andere Kugeln in einer Urne, was ist  also die Wahrscheinlichkeit
also die Wahrscheinlichkeit  aus
aus 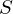 schwarze Kugeln zu ziehn, wenn man
schwarze Kugeln zu ziehn, wenn man  Kugeln zieht?
Kugeln zieht?
Seien
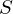 schwarze und
schwarze und  andere Kugeln in einer Urne, was ist
andere Kugeln in einer Urne, was ist  also die Wahrscheinlichkeit
also die Wahrscheinlichkeit  aus
aus 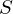 schwarze Kugeln zu ziehn, wenn man
schwarze Kugeln zu ziehn, wenn man  Kugeln zieht?
Kugeln zieht? Bei einer Hypergeometrischen Verteilung wird ohne Zurücklegen gezogen. Die zweite Frage ist ein typischer Fall für eine Hypergeometrische Verteilung.

Die Verallgemeinerung auf mehr als zwei unterschiedliche Arten von Kugeln ist naheliegend: man multipliziert im Zähler die Binomialkoeffizienten für jede Art von Kugeln.

Die Verallgemeinerung auf mehr als zwei unterschiedliche Arten von Kugeln ist naheliegend: man multipliziert im Zähler die Binomialkoeffizienten für jede Art von Kugeln.
Was ist eine geometrische Verteilung?
Man interessiert sich für eine Wahrscheinlichkeit . Was ist damit gemeint und wie berechnet man sie?
. Was ist damit gemeint und wie berechnet man sie?
Was ist und
und  ?
?
Man interessiert sich für eine Wahrscheinlichkeit
 . Was ist damit gemeint und wie berechnet man sie?
. Was ist damit gemeint und wie berechnet man sie?Was ist
 und
und  ?
?Bei einer geometrischen Verteilung gibt es zwei mögliche Ausgänge (meist 0 und 1). Ein Treffer (1) hat die Wahrscheinlichkeit  eine Niete (0) die Wahrscheinlichkeit
eine Niete (0) die Wahrscheinlichkeit  .
.
 bezeichnet hierbei die Wahrscheinlichkeit k 0er vor dem ersten 1er zu erhalten und es gilt
bezeichnet hierbei die Wahrscheinlichkeit k 0er vor dem ersten 1er zu erhalten und es gilt 
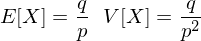
 eine Niete (0) die Wahrscheinlichkeit
eine Niete (0) die Wahrscheinlichkeit  .
.  bezeichnet hierbei die Wahrscheinlichkeit k 0er vor dem ersten 1er zu erhalten und es gilt
bezeichnet hierbei die Wahrscheinlichkeit k 0er vor dem ersten 1er zu erhalten und es gilt 
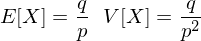
Wann wendet man die Binomialverteilung an? Wie ist die Formel für die Binomialverteilung?
Was ist und
und  ?
?
Was ist
 und
und  ?
?Die Binomialverteilung wird angewendet, wenn man N Experimente mit den gleichen zwei möglichen Ausgängen hat, was man Bernoulli Experimente nennt. Man interessiert sich für die Wahrscheinlichkeit k Treffer in den N Experimenten zu erzielen, welche gegeben ist durch:




Wann verwendet man eine Negative Binomialverteilung?
Was ist die Formel dafür?
Was ist und
und  ?
?
Was ist die Formel dafür?
Was ist
 und
und  ?
?Die Negative Binomialverteilung wird angewendet wenn man die Wahrscheinlichkeit berechnen will k 0er vor dem r-ten 1er zu haben. Diese ist gegeben durch:
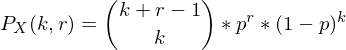

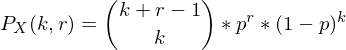

 Wann verwendet man die Poissonverteilung? Wie ist sie definiert? Was sind
Wann verwendet man die Poissonverteilung? Wie ist sie definiert? Was sind  und
und  ?
?Was ist
 ?* Was ist
?* Was ist  ?*
?**
 -Funktion gegeben (Zettel)
-Funktion gegeben (Zettel)
Die Poissonverteilung wird als Annäherung an die Binomialverteilung genutzt, denn es gilt 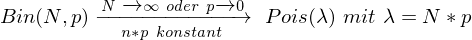


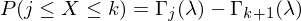

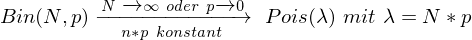


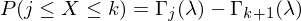

Sei  eine Zufallsvariable auf
eine Zufallsvariable auf  . Die Wahrscheinlichkeitserzeugende Funktion (WEF)
. Die Wahrscheinlichkeitserzeugende Funktion (WEF)  ist definiert als?
ist definiert als?
 eine Zufallsvariable auf
eine Zufallsvariable auf  . Die Wahrscheinlichkeitserzeugende Funktion (WEF)
. Die Wahrscheinlichkeitserzeugende Funktion (WEF)  ist definiert als?
ist definiert als? Die WEF ist eindeutig.
Die WEF ist eindeutig.Definition eines Wahrscheinlichkeitsraums (im stetigen Fall) und der darin vorkommenden Komponenten.
Ein Wahrscheinlichkeitsraum ist ein Tripel 





Was ist eine Dichte?
Eine Dichte auf 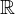 ist eine nicht-negative Funktion
ist eine nicht-negative Funktion  mit
mit  Dabei muss
Dabei muss  stetig bis auf endlich viele Sprungstellen sein, damit das Intergral wohldefiniert ist.
stetig bis auf endlich viele Sprungstellen sein, damit das Intergral wohldefiniert ist.
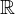 ist eine nicht-negative Funktion
ist eine nicht-negative Funktion  mit
mit  Dabei muss
Dabei muss  stetig bis auf endlich viele Sprungstellen sein, damit das Intergral wohldefiniert ist.
stetig bis auf endlich viele Sprungstellen sein, damit das Intergral wohldefiniert ist.Was ist eine Verteilungsfunktion 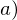 prinzipiell
prinzipiell 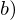 im Zusammenhang zu einer Dichte
im Zusammenhang zu einer Dichte  ? Welche Aussage kann man über eine Verteilungsfunktion und Wahrscheinlichkeit treffen?
? Welche Aussage kann man über eine Verteilungsfunktion und Wahrscheinlichkeit treffen?
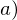 prinzipiell
prinzipiell 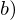 im Zusammenhang zu einer Dichte
im Zusammenhang zu einer Dichte  ? Welche Aussage kann man über eine Verteilungsfunktion und Wahrscheinlichkeit treffen?
? Welche Aussage kann man über eine Verteilungsfunktion und Wahrscheinlichkeit treffen?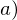 eine Funktion
eine Funktion 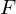 auf
auf 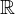 mit Werten in
mit Werten in  heißt Verteilungsfunktion, wenn sie rechtsstetig und monoton wachsend ist und wenn für
heißt Verteilungsfunktion, wenn sie rechtsstetig und monoton wachsend ist und wenn für 
 gilt.
gilt.


 und
und 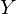 Zufallsvariablen. Die Kovarianz
Zufallsvariablen. Die Kovarianz  von
von  und
und 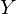 ist definiert als?
ist definiert als? und
und 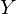 unabhängig. Was gilt für die Kovarianz?
unabhängig. Was gilt für die Kovarianz?
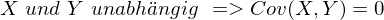
 Zufallsvariable mit Dichte
Zufallsvariable mit Dichte 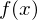 ,
,  eine reellwertige Funktion.
eine reellwertige Funktion.  . Wie bestimmt man die Verteilung und die Dichte von
. Wie bestimmt man die Verteilung und die Dichte von 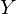 ?
? den Wertebereich von
den Wertebereich von 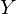 bestimmen
bestimmen die Verteilungsfunktion von
die Verteilungsfunktion von  finden
finden

 eine stetige Zufallsvariable. Was ist die CF von
eine stetige Zufallsvariable. Was ist die CF von  ? (Exponentialfunktion ausformulieren)
? (Exponentialfunktion ausformulieren)Was gilt für die CF einer Summe von u.i.v. ZV?



Die CF der Summe ist das Produkt der einzelnen CFs
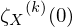

Was besagt die Markov-Ungleichung?
(inklusive Vorraussetzungen)
(inklusive Vorraussetzungen)
 eine stetige ZV mit Dichte
eine stetige ZV mit Dichte 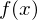 und sei
und sei  eine auf
eine auf  monoton steigende nichtnegative Funktion mit
monoton steigende nichtnegative Funktion mit  dann gilt:
dann gilt:
Tschebyscheff-Ungleichung in der Standardform?
Tschebyscheff-Ungleichung mit ?
?
Tschebyscheff-Ungleichung mit
 ?
? eine stetige ZV mit endlicher Varianz. Für
eine stetige ZV mit endlicher Varianz. Für  :
:

Was bedeutet Konvergenz
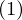 in Verteilung?
in Verteilung?
 in Wahrscheinlichkeit?
in Wahrscheinlichkeit?
 fast sicher?
fast sicher?
Welche Beziehung gilt unter diesen 3 Konvergenzarten?
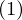 in Verteilung?
in Verteilung? in Wahrscheinlichkeit?
in Wahrscheinlichkeit? fast sicher?
fast sicher?Welche Beziehung gilt unter diesen 3 Konvergenzarten?

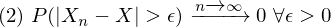
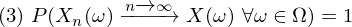

Was besagt das Gesetz der großen Zahlen(Konvergenz in Verteilung)?
 eine Folge u.i.v. ZV mit
eine Folge u.i.v. ZV mit  :
:
Oder mit Worten: Für eine reellwertige Folge u.i.v. ZV mit gleichem endlichen Erwartungswert für jedes Folgenglied konvergiert das arithmetische Mittel der Folge in Verteilung gegen den Erwartungswert.
Was besagt das schwache Gesetz der großen Zahlen?
 unabhängige ZV mit gleichem Erwartungswert und Varianzen
unabhängige ZV mit gleichem Erwartungswert und Varianzen  Dann gilt
Dann gilt  :
: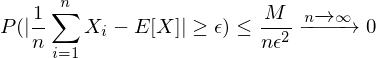
Oder in Worten: Die Wahrscheinlichkeit, dass das arithmetische Mittel von n unabh. ZVen mit gleichem Erwartungswert um mehr als Epsilon vom Erwartungswert abweicht ist kleiner gleich
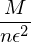 und konvergiert gegen Null.
und konvergiert gegen Null.Was besagt das starke Gesetz der großen Zahlen?
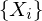 eine Folge unkorrelierter ZV und
eine Folge unkorrelierter ZV und  . Dann konvergiert die Folge
. Dann konvergiert die Folge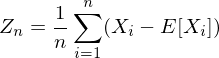
fast sicher gegen 0.
Kartensatzinfo:
Autor: WiMaAux
Oberthema: Mathematik
Thema: Wahrscheinlichkeitsrechnung
Schule / Uni: Universität Augsburg
Ort: Augsburg
Veröffentlicht: 16.04.2012
Schlagwörter Karten:
Alle Karten (62)
keine Schlagwörter







 wenn A und B disjunkt
wenn A und B disjunkt gleich sind?
gleich sind?
 ?
?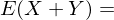 ?
?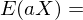 ?
? unabhängig
unabhängig  ?
? ?
?




 inklusive Verschiebungssatz?
inklusive Verschiebungssatz?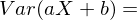 ?
?


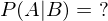

 eine Zerlegung von
eine Zerlegung von  nach dem Satz der totalen Wahrscheinlichkeit?
nach dem Satz der totalen Wahrscheinlichkeit?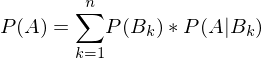

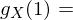
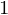










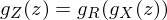
 von
von  -Algebra, falls gilt:
-Algebra, falls gilt: 









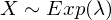
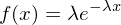





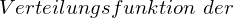



 mit
mit  stetige Zufallsvariable?
stetige Zufallsvariable?








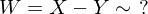




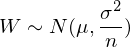



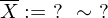 für
für  u.i.v. ZV mit
u.i.v. ZV mit 

 , für
, für  Verteilungen?
Verteilungen?