Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
27
How are Progressive Meshes generated, stored and reconstructed? How can we do Selective Refinement?
Original mesh: 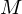
Incremental Decimation applies a series of decimation operators:
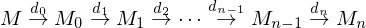
By reversing these operators, we can reconstruct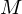 from the decimated mesh
from the decimated mesh 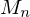
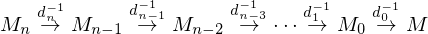
In order to make a Halfedge Collapse operator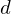 reversible, we need to store:
reversible, we need to store:
Thus, each operator is stored as
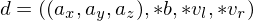
Selective Refinement
If we want to undo an operator
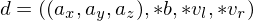
the problem might be that one of the opposite vertices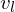 or
or 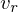 does not exist:
does not exist:
In order to solve this problem, we store the refined mesh as a binary forest where the leaf nodes are the unrefined vertices and each inner node corresponds to a decimation operator.
During decimation, we remember from which original vertices our mesh started out. Initially, we store at every triangle corner a pointer to the incident vertex. As we decimate the mesh, these triangle corner labels remain intact. When we store an operator, instead of storing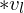 ,
, 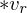 as the vertices in the decimated mesh, we store the values stored in the respective triangle corners.
as the vertices in the decimated mesh, we store the values stored in the respective triangle corners.
If we want to refine at a vertex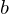 , we find the two opposite vertices
, we find the two opposite vertices 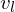 ,
, 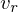 in the currently refined mesh by walking up the binary forest of operators until we find vertices that have already been instantiated.
in the currently refined mesh by walking up the binary forest of operators until we find vertices that have already been instantiated.
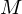
Incremental Decimation applies a series of decimation operators:
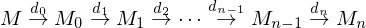
By reversing these operators, we can reconstruct
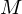 from the decimated mesh
from the decimated mesh 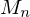
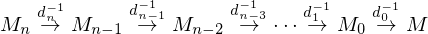
In order to make a Halfedge Collapse operator
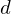 reversible, we need to store:
reversible, we need to store:- Position of the source vertex which was collapsed:

- A pointer to the target vertex towards which
 was collapsed:
was collapsed: 
- Pointers to the two boundary vertices which were adjacent to both
 and
and 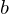 before the collapse:
before the collapse: 
Thus, each operator is stored as
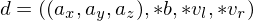
Selective Refinement
If we want to undo an operator
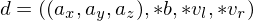
the problem might be that one of the opposite vertices
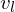 or
or 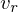 does not exist:
does not exist:-
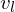 /
/ 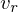 might not exist yet if it is still not expanded
might not exist yet if it is still not expanded -
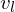 /
/ 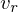 might not exist anymore if it has previously been split
might not exist anymore if it has previously been split
In order to solve this problem, we store the refined mesh as a binary forest where the leaf nodes are the unrefined vertices and each inner node corresponds to a decimation operator.
During decimation, we remember from which original vertices our mesh started out. Initially, we store at every triangle corner a pointer to the incident vertex. As we decimate the mesh, these triangle corner labels remain intact. When we store an operator, instead of storing
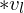 ,
, 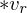 as the vertices in the decimated mesh, we store the values stored in the respective triangle corners.
as the vertices in the decimated mesh, we store the values stored in the respective triangle corners.If we want to refine at a vertex
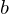 , we find the two opposite vertices
, we find the two opposite vertices 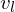 ,
, 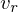 in the currently refined mesh by walking up the binary forest of operators until we find vertices that have already been instantiated.
in the currently refined mesh by walking up the binary forest of operators until we find vertices that have already been instantiated.Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

