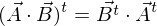Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
3
Im lokalen Koordinatensystem erhält man aus der Orthogonalen Form für ein Element

Wie lautet mit der Transformation die Steifigkeitsmatrix
die Steifigkeitsmatrix  und die Lasspalte
und die Lasspalte  im globalen Koordinatensystem?
im globalen Koordinatensystem?
Hinweis: Für die Transponierung eines Matrizenproduktes gilt allgemein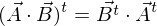

Wie lautet mit der Transformation
 die Steifigkeitsmatrix
die Steifigkeitsmatrix  und die Lasspalte
und die Lasspalte  im globalen Koordinatensystem?
im globalen Koordinatensystem?Hinweis: Für die Transponierung eines Matrizenproduktes gilt allgemein