Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
3
Wann heißt eine Relation (partielle) Ordnung?
Eine Relation R 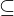 A x A heißt (partielle ) Ordnung, falls folgendes gilt:
A x A heißt (partielle ) Ordnung, falls folgendes gilt:
- Reflexivität: für alle a A gilt (a, a)
A gilt (a, a)  R
R
- Transitivität: falls für beliebige a, b, c A (a, b)
A (a, b)  R und (b, c)
R und (b, c)  R gilt, so muss auch (a,c)
R gilt, so muss auch (a,c)  R gelten.
R gelten.
- Antisymmetrie: falls für beliebige a, b A (a, b)
A (a, b)  R und (b, a)
R und (b, a)  R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.
R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.
Bei der Definition einer Ordnung hat sich gegenüber der Def. einer Äquivalenzrelation nur die letzte Eigenschaft geändert (Antisymmetrie vs. Symmetrie).
Achtung: Antisymmentrie ist nicht das Gegenteil von Symmetrie!
Jede Gleichheitsrelation erfüllt beide Eigenschaften.
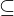 A x A heißt (partielle ) Ordnung, falls folgendes gilt:
A x A heißt (partielle ) Ordnung, falls folgendes gilt:- Reflexivität: für alle a
 A gilt (a, a)
A gilt (a, a)  R
R- Transitivität: falls für beliebige a, b, c
 A (a, b)
A (a, b)  R und (b, c)
R und (b, c)  R gilt, so muss auch (a,c)
R gilt, so muss auch (a,c)  R gelten.
R gelten.- Antisymmetrie: falls für beliebige a, b
 A (a, b)
A (a, b)  R und (b, a)
R und (b, a)  R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.
R gelten, so muss a = b gelten, d.h., a und b sind dann gleich.Bei der Definition einer Ordnung hat sich gegenüber der Def. einer Äquivalenzrelation nur die letzte Eigenschaft geändert (Antisymmetrie vs. Symmetrie).
Achtung: Antisymmentrie ist nicht das Gegenteil von Symmetrie!
Jede Gleichheitsrelation erfüllt beide Eigenschaften.
Karteninfo:
Autor: P-H-I-L
Oberthema: Mathematik
Thema: Mathematische Strukturen
Veröffentlicht: 13.04.2010

