Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
9
D1: Definitionslücken bestimmen und feststellen, ob diese behebbar sind oder nicht, und im zweiten Fall die Gleichung der zugehörigen senkrechten Asymptote angeben.
Hebbare/ Nicht- hebbare Lücken:
Hat das Zählerpolynom bei der Definitionslücke x₀ eine Nullstelle, d.h. z(x) strebt für x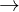
x₀ gegen 0, so liegt eine stetig behebbare Lücke vor. Sie ist auch daran zu erkennen, dass es sowohl im Nenner als auch im Zähler einen Linearfaktor mit gleichem Wert gibt und es gilt:
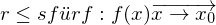
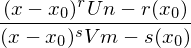
Bsp.: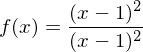
Durch Faktorisieren und anschließendem Kürzen mit (x- x₀) kann der Verlauf des Graphen g der Funktion f in der Nähe der Definitionslücke bestimmt werden. Die Funktion f lässt sich damit an der Stelle x₀ stetig fortsetzen.
Hat das Zählerpolynom bei der Definitionslücke x₀ eine Nullstelle, d.h. z(x) strebt für x
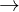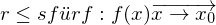
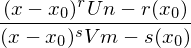
x₀ gegen 0, so liegt eine stetig behebbare Lücke vor. Sie ist auch daran zu erkennen, dass es sowohl im Nenner als auch im Zähler einen Linearfaktor mit gleichem Wert gibt und es gilt: Bsp.:
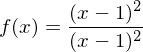
Durch Faktorisieren und anschließendem Kürzen mit (x- x₀) kann der Verlauf des Graphen g der Funktion f in der Nähe der Definitionslücke bestimmt werden. Die Funktion f lässt sich damit an der Stelle x₀ stetig fortsetzen.
Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011