Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
10
Ein Fußball mit der Masse 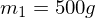 wird mit einem 60° Winkel nach oben geschossen, dabei steckt der Schütze eine Energiemenge von 60
wird mit einem 60° Winkel nach oben geschossen, dabei steckt der Schütze eine Energiemenge von 60 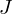 hinein.
hinein.
Wie weit landet der Ball vom Schützen entfernt? (Nicht fertig)
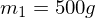 wird mit einem 60° Winkel nach oben geschossen, dabei steckt der Schütze eine Energiemenge von 60
wird mit einem 60° Winkel nach oben geschossen, dabei steckt der Schütze eine Energiemenge von 60 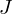 hinein.
hinein.Wie weit landet der Ball vom Schützen entfernt? (Nicht fertig)
Mein Ergebnis: ca. 21,2m entfernt vom Schützden prallt der Ball auf dem Boden auf.
Lösungsweg zu lang, undurchsichtig und nicht unbedingt richtig.
Lösungsansatz: 1. Unabhängigkeitsprinzip
2. Geschwindigkeitsparallelogramm (in diesem Fall rechtwinkliges Dreieck)
3. Trigonometrie (Cosinus)
4. Der Ball hat seinen höchsten Punkt erreicht, wenn der senkrecht gerichtete Teil der Geschwindigkeit durch die Gravitation neutralisiert wurde, also
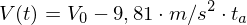
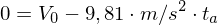
5. Annahme: Keine Reibung etc. und Parabelflug,
->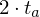 , das gerade ausgerechnet wurde, ist die Gesamtflugzeit t
, das gerade ausgerechnet wurde, ist die Gesamtflugzeit t
6. Einsetzen der Zeit in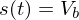 (waagerecht gerichteter Teil der Geschwindigkeit)
(waagerecht gerichteter Teil der Geschwindigkeit) 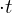
Lösungsweg zu lang, undurchsichtig und nicht unbedingt richtig.
Lösungsansatz: 1. Unabhängigkeitsprinzip
2. Geschwindigkeitsparallelogramm (in diesem Fall rechtwinkliges Dreieck)
3. Trigonometrie (Cosinus)
4. Der Ball hat seinen höchsten Punkt erreicht, wenn der senkrecht gerichtete Teil der Geschwindigkeit durch die Gravitation neutralisiert wurde, also
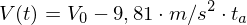
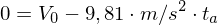
5. Annahme: Keine Reibung etc. und Parabelflug,
->
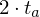 , das gerade ausgerechnet wurde, ist die Gesamtflugzeit t
, das gerade ausgerechnet wurde, ist die Gesamtflugzeit t6. Einsetzen der Zeit in
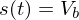 (waagerecht gerichteter Teil der Geschwindigkeit)
(waagerecht gerichteter Teil der Geschwindigkeit)