Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
30
Explain how to use Error Quadrics to compute the closest point to a set of planes!
We can represent a plane by
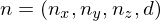
if
and a point by
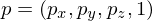
Then, the distance from to the plane is given by
to the plane is given by
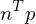
Given a set of planes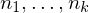 , we want to find a point
, we want to find a point  which minimizes the squared distances to all planes:
which minimizes the squared distances to all planes:
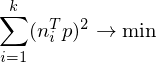
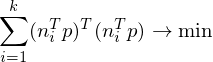
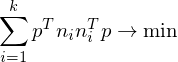
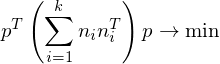
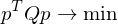
The matrices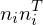 are called fundamental error quadrics and are computed as
are called fundamental error quadrics and are computed as
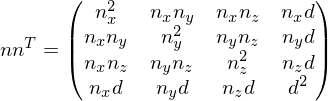
From this definition, we see that the error quadrics of two sets of planes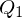 ,
, 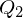 can simply be merged into one error quadric by adding them:
can simply be merged into one error quadric by adding them:
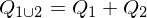
Solution Approach 1
In order to find a minimum solution for , we can find the eigenvector to the smallest eigenvalue of
, we can find the eigenvector to the smallest eigenvalue of 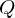 .
.
Solution Approach 2
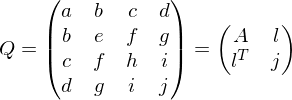
By computing
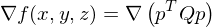
we obtain the linear system
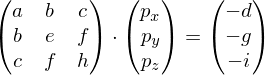
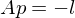
Which is easier to solve than computing the eigenvectors and eigenvalues of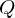 .
.
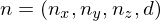
if

and a point by
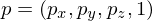
Then, the distance from
 to the plane is given by
to the plane is given by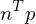
Given a set of planes
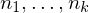 , we want to find a point
, we want to find a point  which minimizes the squared distances to all planes:
which minimizes the squared distances to all planes: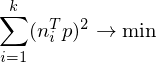
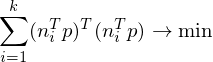
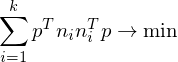
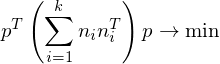
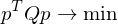
The matrices
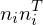 are called fundamental error quadrics and are computed as
are called fundamental error quadrics and are computed as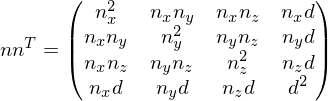
From this definition, we see that the error quadrics of two sets of planes
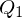 ,
, 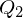 can simply be merged into one error quadric by adding them:
can simply be merged into one error quadric by adding them: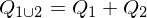
Solution Approach 1
In order to find a minimum solution for
 , we can find the eigenvector to the smallest eigenvalue of
, we can find the eigenvector to the smallest eigenvalue of 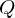 .
.Solution Approach 2
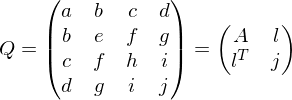
By computing
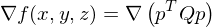
we obtain the linear system
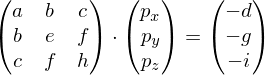
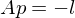
Which is easier to solve than computing the eigenvectors and eigenvalues of
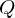 .
.Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

