Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
47
Explain parametrization using Least Squares Conformal Maps!
A parametrization is called conformal iff it is angle-preserving:
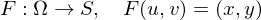
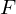 is conformal iff
is conformal iff 
or
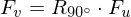
or
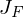 is orthogonal:
is orthogonal:
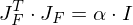
Furthermore, it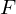 is conformal iff its inverse
is conformal iff its inverse 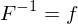 is conformal.
is conformal.
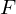 conformal
conformal
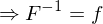 conformal
conformal
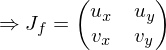 orthogonal
orthogonal
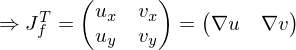 orthogonal
orthogonal
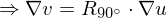
Solve least squares problem
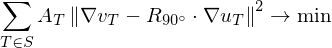
for parameters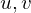 . In order to get a unique solution, fix at least two points.
. In order to get a unique solution, fix at least two points.
Computing Discrete Gradients
Computing
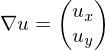
over a triangle given by corner vertices
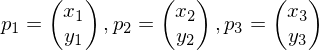
and parameter values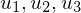 .
.
For a point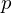 inside the triangle, the interpolated value of
inside the triangle, the interpolated value of 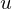 is
is
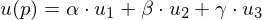
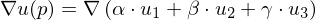
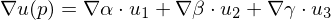
Geometrical derivation of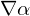 : Consider the triangle edge
: Consider the triangle edge 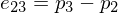 . Along
. Along 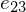 ,
, 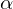 does not change. Along the direction
does not change. Along the direction 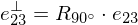 ,
, 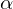 changes most. The magnitude of the change is
changes most. The magnitude of the change is 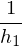 , where
, where 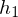 is the height of
is the height of 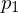 on
on 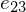 . Thus,
. Thus,
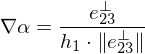
We can compute the height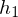 from the triangle area and base length:
from the triangle area and base length:
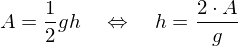
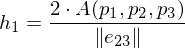
Plugging this result back in gives
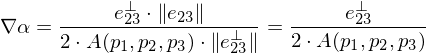
With this result, we get
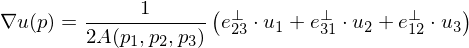
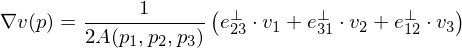
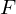 is conformal iff
is conformal iff 
or
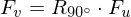
or
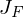 is orthogonal:
is orthogonal: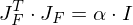
Furthermore, it
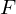 is conformal iff its inverse
is conformal iff its inverse 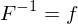 is conformal.
is conformal. conformal
conformal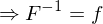 conformal
conformal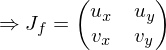 orthogonal
orthogonal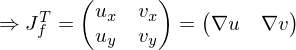 orthogonal
orthogonal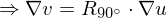
Solve least squares problem
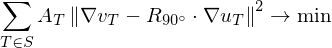
for parameters
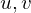 . In order to get a unique solution, fix at least two points.
. In order to get a unique solution, fix at least two points.Computing Discrete Gradients
Computing
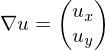
over a triangle given by corner vertices
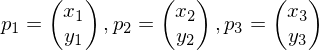
and parameter values
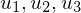 .
.For a point
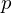 inside the triangle, the interpolated value of
inside the triangle, the interpolated value of 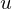 is
is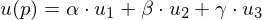
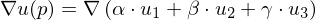
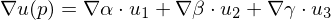
Geometrical derivation of
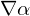 : Consider the triangle edge
: Consider the triangle edge 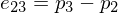 . Along
. Along 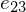 ,
, 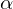 does not change. Along the direction
does not change. Along the direction 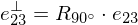 ,
, 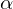 changes most. The magnitude of the change is
changes most. The magnitude of the change is 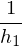 , where
, where 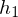 is the height of
is the height of 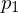 on
on 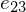 . Thus,
. Thus,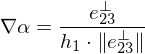
We can compute the height
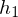 from the triangle area and base length:
from the triangle area and base length: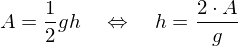
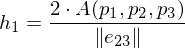
Plugging this result back in gives
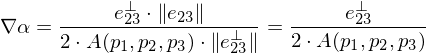
With this result, we get
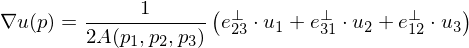
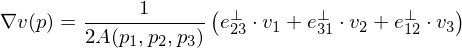
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

