Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
5
Zustände von Prozessen nach wiederholter Durchführung mithilfe der Matrizenmultiplikation berechnen und deuten, insbesondere bei zyklischen Prozessen.
Wird ein Prozess durch eine Matrix beschrieben, dann erhält man aus dem Ausgangsvektor durch Multiplizieren den Vektor des zeitlich nachfolgenden Zustandes und durch wiederholte Multiplikation mit der Matrix die darauf folgenden Zustände. Diese kann man direkt auch dadurch berechnen, dass man - gemäß dem Assoziativgesetz- zunächst die entsprechende Matrixpotenz berechnet und diese dann mit dem Ausgangsvektor multipliziert:
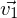 =
=  *
*  ,
, 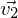 =
= 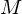 *
* 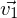 ,
, 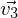 =
=  *
* 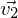 usw. oder
usw. oder 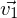 =
=  *
*  ,
,
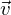 =
= ² *
² *  ,
,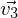 =
=  ³ *
³ *  ...
...
Gilt für irgendeine Matrixpotenz von , dass
, dass 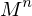 = E(Einheitsmatrix) für
= E(Einheitsmatrix) für 

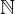 , also
, also 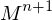 =
= , dann wird durch die Übergangsmatrix
, dann wird durch die Übergangsmatrix  ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
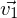 =
=  *
*  ,
, 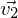 =
= 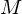 *
* 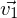 ,
, 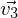 =
=  *
* 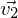 usw. oder
usw. oder 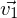 =
=  *
*  ,
,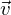 =
= ² *
² *  ,
,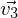 =
=  ³ *
³ *  ...
...Gilt für irgendeine Matrixpotenz von
 , dass
, dass 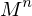 = E(Einheitsmatrix) für
= E(Einheitsmatrix) für 

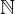 , also
, also 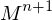 =
= , dann wird durch die Übergangsmatrix
, dann wird durch die Übergangsmatrix  ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.
ein zyklischer Prozess der Länge n beschrieben. Dies bedeutet, dass sich die Folge der Zustandsvektoren jeweils nach n Schritten wiederholt.Karteninfo:
Autor: CoboCards-User
Oberthema: Mathematik
Thema: Mathe-Lk
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 19.03.2011

