Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
70
Wie funktioniert die Newton-Iteration?
Strahl- und Oberflächengleichung gleichsetzen => nichtlineares Nullstellenproblem
Mit der N-I kann dieses angenähert werden:
Sehstrahl = Koordinatenachse x
Startpunkt -> Punkt x1 in Nähe des gesuchten Nullpunkts: Approximierung durch viele kleine Bounding Volumes um Fläche. Strahl mit diesen schneiden um x1 zu bestimmen.
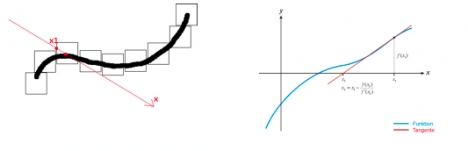
Man berechnet an der Stelle x1 jetzt die Tangente, da wo die Tangente die x-Achse schneidet, berechnet man den Funtionswert und hat einen neuen Schätzwert x2. Iteration bis die Funktion an der Stelle einen sehr kleinen Wert annimmt, sich der Schätzwert nicht mehr groß ändert, oder ein Maximum an n Iterationen überschritten wurde.
Möglichst eng anliegende, kleine BVs um Teile der Fläche bilden um gute Startwerte für das iterative Verfahren zu haben, wird sonst unperformant oder konvergiert nicht.
Macht man allerdings zu viele kleine BVs wird der Aufwand für die Schnitttests mit den BVs unverhältnismäßig hoch. Das richtige Verhältnis zwischen Aufwand für Newton Iteration und die BV Schnitttests muss man also abwägen.
Mit der N-I kann dieses angenähert werden:
Sehstrahl = Koordinatenachse x
Startpunkt -> Punkt x1 in Nähe des gesuchten Nullpunkts: Approximierung durch viele kleine Bounding Volumes um Fläche. Strahl mit diesen schneiden um x1 zu bestimmen.
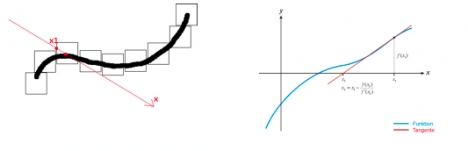
Man berechnet an der Stelle x1 jetzt die Tangente, da wo die Tangente die x-Achse schneidet, berechnet man den Funtionswert und hat einen neuen Schätzwert x2. Iteration bis die Funktion an der Stelle einen sehr kleinen Wert annimmt, sich der Schätzwert nicht mehr groß ändert, oder ein Maximum an n Iterationen überschritten wurde.
Möglichst eng anliegende, kleine BVs um Teile der Fläche bilden um gute Startwerte für das iterative Verfahren zu haben, wird sonst unperformant oder konvergiert nicht.
Macht man allerdings zu viele kleine BVs wird der Aufwand für die Schnitttests mit den BVs unverhältnismäßig hoch. Das richtige Verhältnis zwischen Aufwand für Newton Iteration und die BV Schnitttests muss man also abwägen.
Karteninfo:
Autor: cobocards-admin
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: Universität Koblenz-Landau
Ort: Koblenz
Veröffentlicht: 18.10.2010

