Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
76
Explain the de Casteljau algorithm!
de Casteljau algorithm gives a geometric procedure to construct points on Bézier curves.
Example: Given control points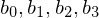 (cubic spline), we compute
(cubic spline), we compute
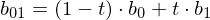
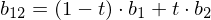
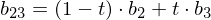
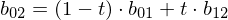
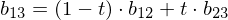
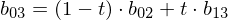
Note how this schema iteratively evaluates the Bernstein polynomials for all coefficients:
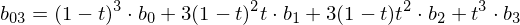
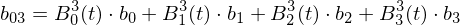
Useful properties:
Example: Given control points
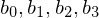 (cubic spline), we compute
(cubic spline), we compute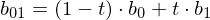
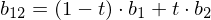
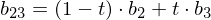
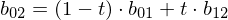
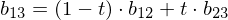
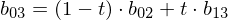
Note how this schema iteratively evaluates the Bernstein polynomials for all coefficients:
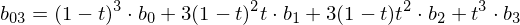
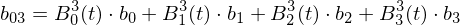
Useful properties:
- Numerically robust: Sequence of affine combinations (instead of sum of scaled polynomial coefficients)
- First derivative:

Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

