Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
14
G3: Parameterdarstellung für Ebenen aus drei Punkten ermitteln sowie überprüfen, ob ein Punkt auf einer gegebenen Ebene liegt (Punktprobe) und die Ergebnisse im Sachzusammenhang interpretieren.
Parameterdarstellung für Ebenen mit drei Punkten:
Die Gleichung einer Ebene E mit dem Stützvektor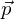 und den Spannvektoren
und den Spannvektoren 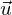 und
und 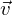 lautet:
lautet:
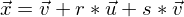 ; r, s ∈ R.
; r, s ∈ R.
E ist festgelegt durch die Punkte A, B und C:
Stützvektor: Ortsvektor von A
Spannvektoren: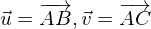
Punktprobe für den Punkt D:
Setzt man die Koordinaten für D in die Gleichung für E ein, erhält man ein LGS mit drei linearen Gleichungen für zwei Variablen r und s.
Aus zwei Gleichungen erhält man Werte für r und s; erfüllen diese Werte auch die dritte Gleichung liegt der Punkt D in E.
Die Gleichung einer Ebene E mit dem Stützvektor
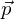 und den Spannvektoren
und den Spannvektoren 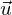 und
und 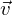 lautet:
lautet: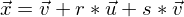 ; r, s ∈ R.
; r, s ∈ R.E ist festgelegt durch die Punkte A, B und C:
Stützvektor: Ortsvektor von A
Spannvektoren:
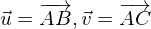
Punktprobe für den Punkt D:
Setzt man die Koordinaten für D in die Gleichung für E ein, erhält man ein LGS mit drei linearen Gleichungen für zwei Variablen r und s.
Aus zwei Gleichungen erhält man Werte für r und s; erfüllen diese Werte auch die dritte Gleichung liegt der Punkt D in E.
Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011

