Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
106
Characterize linear, affine and projective transforms!
Linear Maps
A map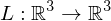 which is
which is
additive: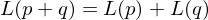
homogenous: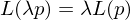
Representable by a transformation matrix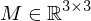 :
:
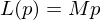
Linear map preserve the origin.
Affine Maps
A map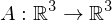 which is
which is
composed of a linear map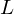 and a translation:
and a translation:

Affine transformations can be represented as a matrix-vector product by using extended coordinates:
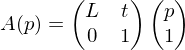
Affine maps preserve collinearity of points and distance ratios.
Projective Maps
Represented by a matrix-vector product using homogeneous coordinates.
Projective maps preserve cross ratios:
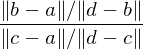
A map
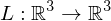 which is
which isadditive:
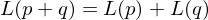
homogenous:
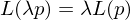
Representable by a transformation matrix
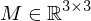 :
: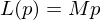
Linear map preserve the origin.
Affine Maps
A map
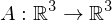 which is
which iscomposed of a linear map
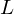 and a translation:
and a translation:
Affine transformations can be represented as a matrix-vector product by using extended coordinates:
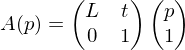
Affine maps preserve collinearity of points and distance ratios.
Projective Maps
Represented by a matrix-vector product using homogeneous coordinates.
Projective maps preserve cross ratios:
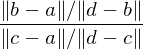
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

