Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
100
Explain how to transform geometry according to camera position and projection to the screen!
Concatenation of three matrices:
Look-at transform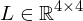
Given a camera position
, a desired viewing direction 
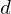and an up vector 
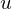, we compute a orthogonal coordinate system as follows:
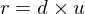
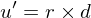
Now, the matrix transforming points from camera space to world space is given by
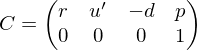
The look-at transform is the inverse of this, transforming points from world space to local camera space:
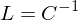
Frustum transform
Transforms points from a frustum defined by the near / far plane distance of the camera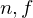
and the extents of the near plane rectangle 
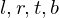into the unit cube 
. 
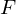maps points on the near plane to 
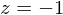and points on the far plane to 
.
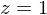Viewport transform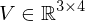
Transforms from the unit cube to pixel coordinates on a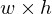
screen:
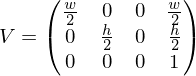
Look-at transform
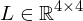
Given a camera position
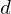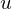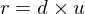
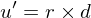
, a desired viewing direction and an up vector , we compute a orthogonal coordinate system as follows:Now, the matrix transforming points from camera space to world space is given by
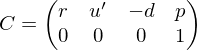
The look-at transform is the inverse of this, transforming points from world space to local camera space:
Frustum transform
Transforms points from a frustum defined by the near / far plane distance of the camera
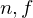and the extents of the near plane rectangle 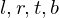into the unit cube . 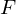maps points on the near plane to 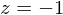and points on the far plane to 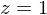.Viewport transform
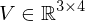
Transforms from the unit cube to pixel coordinates on a
screen: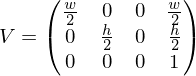
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022