Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
16
f invariante Unterräume
1.1 Sei  also
also  . Ein UR
. Ein UR  von
von  heißt f-invariant, wenn gilt
heißt f-invariant, wenn gilt  .
.
1.2 Bemerkungen_ sind stets f-invariant.
sind stets f-invariant.
Ist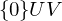 f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von
f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von  . Sei
. Sei  Basis von
Basis von  , ergänze
, ergänze  zu Basis
zu Basis  von
von  . Bzgl. dieser Basis hat
. Bzgl. dieser Basis hat  eine Matrix
eine Matrix 
1.3 Lemma: Seine vertauschbar, d.h.
vertauschbar, d.h.  . Dann sind
. Dann sind  f-invariante URe. Inbesondere sind alle Eigenräume von
f-invariante URe. Inbesondere sind alle Eigenräume von 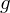 f-invariant.
f-invariant.
(Natürlich ohne Einschränkungen: Also alle Eigenräume von sind g-invariant.
sind g-invariant.
 also
also  . Ein UR
. Ein UR  von
von  heißt f-invariant, wenn gilt
heißt f-invariant, wenn gilt  .
.1.2 Bemerkungen_
 sind stets f-invariant.
sind stets f-invariant.Ist
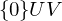 f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von
f-invariant, so ist dies ein erster Schritt zu einer "einfachen" Matrixdarstellung von  . Sei
. Sei  Basis von
Basis von  , ergänze
, ergänze  zu Basis
zu Basis  von
von  . Bzgl. dieser Basis hat
. Bzgl. dieser Basis hat  eine Matrix
eine Matrix 
1.3 Lemma: Seine
 vertauschbar, d.h.
vertauschbar, d.h.  . Dann sind
. Dann sind  f-invariante URe. Inbesondere sind alle Eigenräume von
f-invariante URe. Inbesondere sind alle Eigenräume von 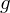 f-invariant.
f-invariant.(Natürlich ohne Einschränkungen: Also alle Eigenräume von
 sind g-invariant.
sind g-invariant.Tags:
Quelle: Skript Scheiderer BII I §1 Hauptaumzerlegung Def.1.1, Bem.1.2
Quelle: Skript Scheiderer BII I §1 Hauptaumzerlegung Def.1.1, Bem.1.2

