Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
5
Explain Parametrization-Based Quad Meshing (Mixed Integer Quadrangulation)
Input: Mesh of triangles 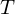 . For some triangles, we have a confident estimate of the local min / max curvature directions (e.g. computed using the Shape Operator) given by an angle
. For some triangles, we have a confident estimate of the local min / max curvature directions (e.g. computed using the Shape Operator) given by an angle 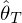 relative to some reference edge
relative to some reference edge 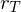 .
.
Smooth Cross Field
We propagate a smooth cross field over the entire surface. For each edge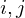 we can define a smoothness energy
we can define a smoothness energy
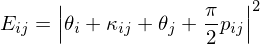
where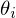 and
and 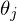 are the cross field directions given as an angle with the reference edges
are the cross field directions given as an angle with the reference edges 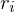 and
and 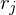 , respectively.
, respectively. 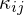 denotes the angle between the two reference edges.
denotes the angle between the two reference edges.
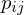 is an integer variable that allows
is an integer variable that allows 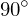 rotations of the cross fields.
rotations of the cross fields.
For the entire mesh, we construct the system
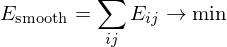
We solve this system for the real variables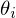 and the integer variables
and the integer variables 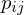 . For those triangles where an input cross field direction is known, we fix the value:
. For those triangles where an input cross field direction is known, we fix the value: 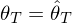 .
.
Parametrization
For each triangle corner in the mesh, compute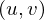 coordinates such that for each triangle,
coordinates such that for each triangle,
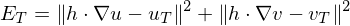
becomes small. Globally:
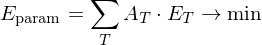
In order to obtain a disk topology for parametrization, the surface needs to be cut open. As an additional constraint, we thus introduce the requirement, that the parametrization should be consistent across boundary edges. That means that the transformation of parameters across an edge should be a grid automorphism.
Specifically, given a boundary edge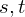 between two triangles
between two triangles 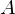 and
and 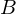 we constrain the
we constrain the 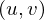 coordinates at the opposite sides of the vertices
coordinates at the opposite sides of the vertices 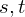 to be equal up to grid automorphisms. That means:
to be equal up to grid automorphisms. That means:
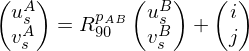
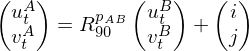
The integer variable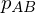 is known from the smooth cross field. For
is known from the smooth cross field. For 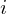 ,
, 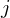 , we need to find integer solutions.
, we need to find integer solutions.
In order to ensure that the resulting mesh will be a quad mesh, we snap singularities to integer positions.
We can introduce additional hard alignment constraints in order to snap feature edges to integer iso-lines. If an edge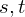 should be snapped to a
should be snapped to a 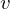 -integer-iso-line, we constrain the values of
-integer-iso-line, we constrain the values of 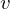 for vertices of
for vertices of 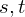 to be integer.
to be integer.
Solving Mixed-Integer Problems
In general: NP-Hard. We approximate a solution by relaxing the problem: Find a real-valued solution. Snap integer variables to nearest possible value, repeat.
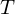 . For some triangles, we have a confident estimate of the local min / max curvature directions (e.g. computed using the Shape Operator) given by an angle
. For some triangles, we have a confident estimate of the local min / max curvature directions (e.g. computed using the Shape Operator) given by an angle 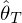 relative to some reference edge
relative to some reference edge 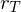 .
.Smooth Cross Field
We propagate a smooth cross field over the entire surface. For each edge
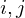 we can define a smoothness energy
we can define a smoothness energy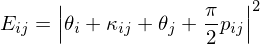
where
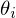 and
and 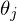 are the cross field directions given as an angle with the reference edges
are the cross field directions given as an angle with the reference edges 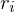 and
and 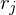 , respectively.
, respectively. 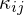 denotes the angle between the two reference edges.
denotes the angle between the two reference edges.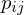 is an integer variable that allows
is an integer variable that allows 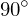 rotations of the cross fields.
rotations of the cross fields.For the entire mesh, we construct the system
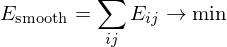
We solve this system for the real variables
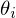 and the integer variables
and the integer variables 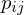 . For those triangles where an input cross field direction is known, we fix the value:
. For those triangles where an input cross field direction is known, we fix the value: 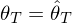 .
.Parametrization
For each triangle corner in the mesh, compute
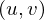 coordinates such that for each triangle,
coordinates such that for each triangle,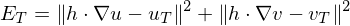
becomes small. Globally:
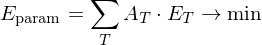
In order to obtain a disk topology for parametrization, the surface needs to be cut open. As an additional constraint, we thus introduce the requirement, that the parametrization should be consistent across boundary edges. That means that the transformation of parameters across an edge should be a grid automorphism.
Specifically, given a boundary edge
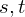 between two triangles
between two triangles 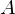 and
and 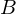 we constrain the
we constrain the 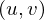 coordinates at the opposite sides of the vertices
coordinates at the opposite sides of the vertices 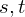 to be equal up to grid automorphisms. That means:
to be equal up to grid automorphisms. That means: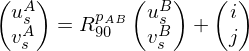
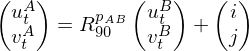
The integer variable
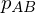 is known from the smooth cross field. For
is known from the smooth cross field. For 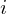 ,
, 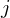 , we need to find integer solutions.
, we need to find integer solutions.In order to ensure that the resulting mesh will be a quad mesh, we snap singularities to integer positions.
We can introduce additional hard alignment constraints in order to snap feature edges to integer iso-lines. If an edge
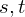 should be snapped to a
should be snapped to a 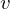 -integer-iso-line, we constrain the values of
-integer-iso-line, we constrain the values of 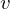 for vertices of
for vertices of 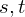 to be integer.
to be integer.Solving Mixed-Integer Problems
In general: NP-Hard. We approximate a solution by relaxing the problem: Find a real-valued solution. Snap integer variables to nearest possible value, repeat.
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

