Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
61
Derive the formula for Monte Carlo Integration! When does MCI converge fast?
Given: values 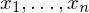 distributed according to
distributed according to 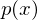
and samples of a function :
: 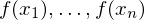
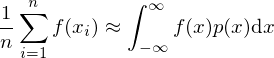
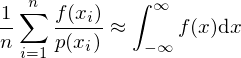
The more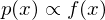 , the smaller the variance of the quotient
, the smaller the variance of the quotient
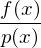 ,
,
thus MCI converges faster.
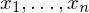 distributed according to
distributed according to 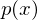
and samples of a function
 :
: 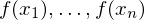
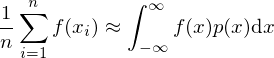
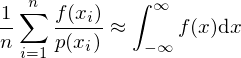
The more
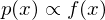 , the smaller the variance of the quotient
, the smaller the variance of the quotient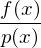 ,
,thus MCI converges faster.
Karteninfo:
Autor: janisborn
Oberthema: Informatik
Thema: Computergrafik
Schule / Uni: RWTH Aachen
Ort: Aachen
Veröffentlicht: 18.05.2022

