Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
31
Beweis: D ist nicht rekursiv
Widerspruchsbeweis:
- nehme an D sei rekursiv
- dann gibt es TM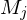 , die D entscheidet
, die D entscheidet
- wende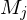 auf
auf 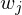 an
an
1.Fall: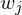 liegt in D
liegt in D
- dann aktzeptiert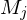 die Eingabe
die Eingabe 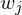 , weil
, weil 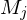 die Sprache entscheidet
die Sprache entscheidet
- Wegen der Definition von D kann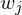 aber nicht in D liegen
aber nicht in D liegen 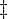
2.Fall: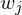 liegt nicht in D
liegt nicht in D
- dann verwirft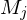 die Eingabe
die Eingabe 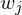 , weil
, weil 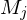 die Sprache entscheidet
die Sprache entscheidet
- Wegen der Definition von D muss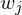 aber in D liegen
aber in D liegen 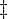
- nehme an D sei rekursiv
- dann gibt es TM
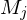 , die D entscheidet
, die D entscheidet- wende
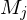 auf
auf 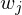 an
an1.Fall:
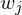 liegt in D
liegt in D- dann aktzeptiert
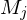 die Eingabe
die Eingabe 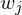 , weil
, weil 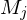 die Sprache entscheidet
die Sprache entscheidet- Wegen der Definition von D kann
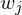 aber nicht in D liegen
aber nicht in D liegen 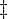
2.Fall:
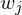 liegt nicht in D
liegt nicht in D- dann verwirft
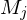 die Eingabe
die Eingabe 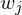 , weil
, weil 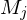 die Sprache entscheidet
die Sprache entscheidet- Wegen der Definition von D muss
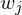 aber in D liegen
aber in D liegen