Zu dieser Karteikarte gibt es einen kompletten Satz an Karteikarten. Kostenlos!
13
G2: Geraden auf ihre gegenseitige Lage untersuchen und möglicherweise vorhandene Schnittpunkte bestimmen. Beispiele:
Als Beispiel für zwei Geraden sei gegeben: Gerade 1 mit 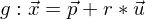 und Gerade 2 mit
und Gerade 2 mit 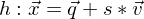
Zu Fall a)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  oder
oder 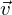 ) linear unabhängig zur Differenz der Aufpunktvektoren (
) linear unabhängig zur Differenz der Aufpunktvektoren (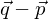 )ist.
)ist.
Zu Fall b)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  und
und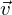 ) linear abhängig zur Differenz der Aufpunktvektoren (
) linear abhängig zur Differenz der Aufpunktvektoren (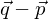 ) ist.
) ist.
Zu Fall c)
Zwei Geraden schneiden sich, ihre Richtungsvektoren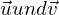 linear unabhängig sind und beide Richtungsvektoren
linear unabhängig sind und beide Richtungsvektoren  und
und  linear abhängig zur Differenz der Aufpunktvektoren (
linear abhängig zur Differenz der Aufpunktvektoren (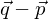 ) sind.
) sind.
Zu Fall d)
Zwei Geraden sind windschief, wenn sowohl Richtungsvektoren und
und  linear unabhängig sind, als auch beide Richtungsvektoren
linear unabhängig sind, als auch beide Richtungsvektoren  und
und  linear unabhängig zur Differenz der Aufpunktvektoren (
linear unabhängig zur Differenz der Aufpunktvektoren (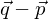 ) sind.
) sind.
g und h schneiden sich in einem Punkt, wenn die Vektorgleichung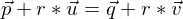 genau eine Lösung (r₀, t₀) hat.
genau eine Lösung (r₀, t₀) hat.
g und h sind identisch, wenn die Vektorgleichung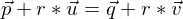 unendlich viele Lösungen hat.
unendlich viele Lösungen hat.
g und h haben keinen gemeinsamen Punkt, wenn die Vektorgleichung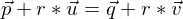 keine Lösung hat.
keine Lösung hat.
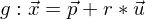 und Gerade 2 mit
und Gerade 2 mit 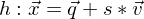
Zu Fall a)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren
 und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  oder
oder 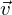 ) linear unabhängig zur Differenz der Aufpunktvektoren (
) linear unabhängig zur Differenz der Aufpunktvektoren (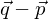 )ist.
)ist. Zu Fall b)
Zwei Geraden sind echt parallel, wenn ihre Richtungsvektoren
 und
und  linear abhängig sind und ein Richtungsvektor (entweder
linear abhängig sind und ein Richtungsvektor (entweder  und
und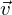 ) linear abhängig zur Differenz der Aufpunktvektoren (
) linear abhängig zur Differenz der Aufpunktvektoren (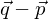 ) ist.
) ist.Zu Fall c)
Zwei Geraden schneiden sich, ihre Richtungsvektoren
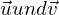 linear unabhängig sind und beide Richtungsvektoren
linear unabhängig sind und beide Richtungsvektoren  und
und  linear abhängig zur Differenz der Aufpunktvektoren (
linear abhängig zur Differenz der Aufpunktvektoren (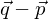 ) sind.
) sind.Zu Fall d)
Zwei Geraden sind windschief, wenn sowohl Richtungsvektoren
 und
und  linear unabhängig sind, als auch beide Richtungsvektoren
linear unabhängig sind, als auch beide Richtungsvektoren  und
und  linear unabhängig zur Differenz der Aufpunktvektoren (
linear unabhängig zur Differenz der Aufpunktvektoren (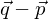 ) sind.
) sind.g und h schneiden sich in einem Punkt, wenn die Vektorgleichung
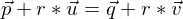 genau eine Lösung (r₀, t₀) hat.
genau eine Lösung (r₀, t₀) hat. g und h sind identisch, wenn die Vektorgleichung
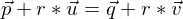 unendlich viele Lösungen hat.
unendlich viele Lösungen hat.g und h haben keinen gemeinsamen Punkt, wenn die Vektorgleichung
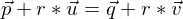 keine Lösung hat.
keine Lösung hat.Karteninfo:
Autor: Exinator
Oberthema: Mathematik
Thema: Abiturvorbereitung
Schule / Uni: MGS
Ort: Schwelm
Veröffentlicht: 28.03.2011

