C3: Mittelwerte von kontinuierlich veränderten Größen mit der Integralrechnung berechnen.
Man nutzt Integralrechnung, um den Mittelwert M einer (stetigen) Funktion im Intervall [a;b] zu berechnen. Dazu teilt man das Integral in diesem Intervall durch die Differenz von b und a.
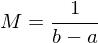
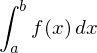
Beispiel: Berechnen Sie den durchschnittlichen Funktionswert der Funktion f mit:
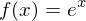(x Element der reellen Zahlen)
im Intervall von 0 bis 3.
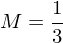
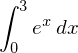
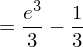
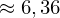
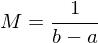
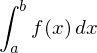
Beispiel: Berechnen Sie den durchschnittlichen Funktionswert der Funktion f mit:
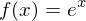(x Element der reellen Zahlen)im Intervall von 0 bis 3.
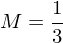
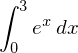
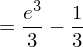
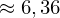
H2: Den Flächeninhalt eines Dreiecks und das Volumen eines Tetraeders nach elementaren Methoden bestimmen.
Der Flächeninhalt A eines Dreiecks ABC entspricht der Hälfte der Länge des Kreuzprodukts zweier Vektoren, die dieses Dreieck aufspannen.
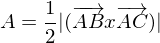
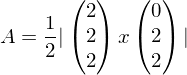
Beispiel: Gesucht ist der Flächeninhalt des Dreiecks ABC mit A(0/0/0), B(2/2/2) und C(0/2/2). Für A ergibt sich:
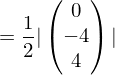
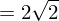
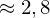
Ein Tetraeder ist eine Pyramide mit einer dreieckigen Grundfläche, bei der alle Seiten gleichlang sind.
Für das Volumen V gilt allgemein:
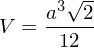
Als Beispiel nehmen wir einen Tetraeder ABCD mit den Eckpunkten A (1/1/1), B (1/0/0), C (0/1/0) und D (0/0/1).
Für das Volumen V ergibt sich:
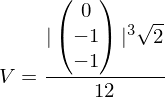
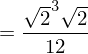
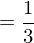
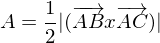
Beispiel: Gesucht ist der Flächeninhalt des Dreiecks ABC mit A(0/0/0), B(2/2/2) und C(0/2/2). Für A ergibt sich:
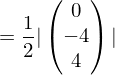
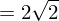
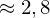
Ein Tetraeder ist eine Pyramide mit einer dreieckigen Grundfläche, bei der alle Seiten gleichlang sind.
Für das Volumen V gilt allgemein:
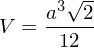
Als Beispiel nehmen wir einen Tetraeder ABCD mit den Eckpunkten A (1/1/1), B (1/0/0), C (0/1/0) und D (0/0/1).
Für das Volumen V ergibt sich:
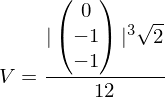
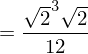
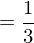
H3: Den Abstand eines Punktes von einer Ebene berechnen.
Der Abstand d eines Punktes Q zur Ebene E (mit dem Punkt P und dem Normalvektor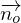 
(Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.
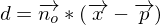
Beispiel: Welchen Abstand hat Q (5/3/1) zur
-Ebene?
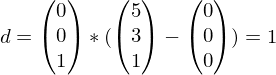
Hinweis: Auch andere Methoden, wie das Benutzen einer zu E senkrechten Geraden durch Q, um den zu Q nächsten Punkt in E zu finden, können benutzt werden.
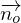(Länge = 1LE)) lässt sich am einfachsten mit der HNF (Hesse'sche Normalenform) berechnen.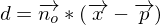Beispiel: Welchen Abstand hat Q (5/3/1) zur
-Ebene?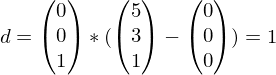Hinweis: Auch andere Methoden, wie das Benutzen einer zu E senkrechten Geraden durch Q, um den zu Q nächsten Punkt in E zu finden, können benutzt werden.
Kartensatzinfo:
Autor: CoboCards-User
Oberthema: Mathematik
Thema: R³, Funktionen
Veröffentlicht: 24.02.2011
Tags: Neizert
Schlagwörter Karten:
Alle Karten (5)
keine Schlagwörter
