Polyeder
richtig
- kein Polyederkegel ist ein Polytop
- jedes Polytop ist konvex
- ein Polyeder, das in einer Kugel mit endlichem Radius ist, ist ein Polytop
falsch
- die Menge der Konvexkombinationen von sechs Punkten hat mindestens fünf Ecken
- ein Polyederkegel hat mindestens zwei Ecken
- kein Polyederkegel ist ein Polytop
- jedes Polytop ist konvex
- ein Polyeder, das in einer Kugel mit endlichem Radius ist, ist ein Polytop
falsch
- die Menge der Konvexkombinationen von sechs Punkten hat mindestens fünf Ecken
- ein Polyederkegel hat mindestens zwei Ecken
Matrix - Sonderformen
| quadratische Matrix | m=n |
| Diagonalmatrix | höchstens in Hauptdiagonale Elemente ungleich 0 |
| Nullmatrix | alle Elemente gleich 0 |
| Einheitsmatrix | Diagonalmatrix mit Hauptdiagonale = 1 |
| untere Dreiecksmatrix | Elemente oberhalb Diagonale = 0 |
| obere Dreiecksmatrix | Elemente unterhalb Diagonale = 0 |
Differentialgleichungen
| Ordnung | höchste vorkommende Ableitung |
| linear | Terme mit y nur in einfacher Potenz |
| homogen | nur y und seinen Ableitungen, keine x oder Konstanten |
| explizit | nach der höchsten Ableitung von y aufgelöst |
| konstante Koeffizienten | nur mit Zahlen, nicht mit anderen Variablen verknüpft |
| mit getrennten Variablen | auf einer Seite je nur x bzw. y |
| exakte (totale) DGL |  mit mit 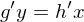 |
| Ähnlichkeits-DGL | 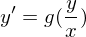 |
Änderungsraten und Elastizitäten
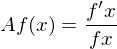
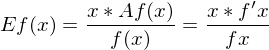
| elastisch | E>1 |
| unelastisch | E<1 |
| proportional-elastisch | E=1 |
Rohstoffverbrauchsmatrix
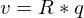
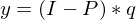
| R | Rohstoffverbrauchsmatrix |
| q | Produktionsvektor |
| v | Rohstoffverbrauch |
| P | Produktionskoeffizientenmatrix |
}
Folgen
| arithmetisch | Addition oder Subtraktion einer Konstante d |
| geometrisch | Multiplikation oder Divison mit einer Konstante |
Basis
Menge von Vektoren, durch deren Linearkombination sich alle Vektoren des Vektorraums darstellen lassen
l.u. Basisvektoren spannen den Raum auf
l.u. Basisvektoren spannen den Raum auf
Eigenwerte
Die Eigenwerte einer Matrix sind Wurzeln des charakteristischen Polynoms der Matrix.
1 ist der Eigenwert jeder Einheitsmatrix.
Eigenwerte symmetrischer Matrizen sind reelle Zahlen.
Zu jeder symmetrischen Matrix gibt es eine ortohormale Basis von Eigenvektoren.
Zu jeder symmetrischen Matrix gibt es Eigenwerte.
Eigenvektoren zu verschiedenen Eigenwerten ein symmetrischen Matrix sind orthogonal.
1 ist der Eigenwert jeder Einheitsmatrix.
Eigenwerte symmetrischer Matrizen sind reelle Zahlen.
Zu jeder symmetrischen Matrix gibt es eine ortohormale Basis von Eigenvektoren.
Zu jeder symmetrischen Matrix gibt es Eigenwerte.
Eigenvektoren zu verschiedenen Eigenwerten ein symmetrischen Matrix sind orthogonal.
Input-Output-Analyse
| q | Bruttobedarfsvektor = Vektor der Produktionsmengen 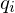 |
| y | Vektor der Verkaufsmengen |
| P | 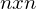 Matrix der Produktionskoeffizienten Matrix der Produktionskoeffizienten 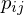 |
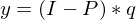
Nettobedarfsvektor
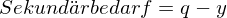
Bedingung für invertierbare Matrix (regulär)
Determinante ist ungleich 0
Matrix hat vollen Rang
Gleichungssystem ist eindeutig lösbar
Matrix hat vollen Rang
Gleichungssystem ist eindeutig lösbar
Differenzierbarkeit
richtig
- ist eine Funktion an einer Stelle differenzierbar, ist so dort auch stetig
- jedes Polynom ist über ganz R differenzierbar
- das Produkt von zwei Polynomen ist über ganz R differenzierbar
- jede konstante Funktion ist über ihren Definitionsbereich differenzierbar
falsch
- ist eine Funktion an der Stelle a stetig, so ist sie dort auch differenzierbar
- jede streng monoton steigende Funktion ist über ganz -r differenzierbar
- ist eine Funktion an einer Stelle differenzierbar, ist so dort auch stetig
- jedes Polynom ist über ganz R differenzierbar
- das Produkt von zwei Polynomen ist über ganz R differenzierbar
- jede konstante Funktion ist über ihren Definitionsbereich differenzierbar
falsch
- ist eine Funktion an der Stelle a stetig, so ist sie dort auch differenzierbar
- jede streng monoton steigende Funktion ist über ganz -r differenzierbar
Kartensatzinfo:
Autor: professor78
Oberthema: Mathematik
Schule / Uni: FernUniversität Hagen
Veröffentlicht: 04.03.2010
Schlagwörter Karten:
Alle Karten (21)
keine Schlagwörter







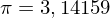
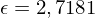

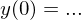

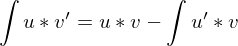

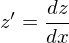

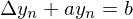
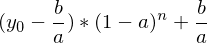
 und
und