Differentialgleichung
- gewöhnliche DGL: Ableitung nach einer einzigen Koordinate (Raum oder Zeit) mit Anfangsbedingungen
- partielle Differentialgleichung: Ableitung nach mehreren Koordinaten (zwei oder mehr Raumkoordinaten, Raum und Zeit) mit Anfangs- und Randbedingungen (Dirichlet)
Finite Differenzen Methode
- pDGL wird in Differenzensterne umgewandelt, welche zu algebraischen Gleichungen in den Unbekannten an den Knoten (nicht unbedingt äquidistant) führen
- Ableitungen durch Differenzenausdrücke approximiert
- Taylorreihenentwicklung
- Vorwärts-, Rückwärts-, Zentrale Differenzen bilden
Bestimmung von Differenz-Ausdrücken
Taylorreihenentwicklung:
Die Taylorreihen so addieren, dass
1. alle Ableitungen niedriger als die gesuchte wegfallen,
2. und möglichst viele Ableitungen höher als die gesuchte wegfallen.
Die Taylorreihen so addieren, dass
1. alle Ableitungen niedriger als die gesuchte wegfallen,
2. und möglichst viele Ableitungen höher als die gesuchte wegfallen.
Möglichkeiten bei der Auswahl des FD-Schemas
- Anzahl der Stützpunkte
- vorwärts, rückwärts, oder zentral
- Auswahl der Knoten (nicht unbedingt äquidistant)
Zeitdiskretisierungsmethoden
Explizites Euler-Verfahren (Euler-Vorwärts-Verfahren):  Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren):
Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren): 
- Vorwärtsdifferenzen
- räumliche Ableitung zum Zeitpunkt n auswerten
- 1. Ordnung genau
- bedingt stabil, zwei Stützstellen
 Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren):
Implizites Euler-Verfahren (Euler-Rückwärts-Verfahren): - Rückwärtsdifferenzen
- räumliche Ableitung zum Zeitpunkt n+1 auswerten
- Gleichungssystem muss für jeden Zeitschritt gelöst werden
- 1. Ordnung genau
- unbeschränkt stabil, zwei Stützstellen

Vorteile Zentraler Differenzen
haben eine höhere Genauigkeitsordnung als einseitige Differenzen mit derselben Anzahl an Funktionswerten
Hauptsatz der Variationsrechnung
garantiert, dass die Lösung der starken Formulierung, sofern sie existiert, der Lösung der schwachen Formulierung entspricht
Schwache Formulierung aufstellen

1. Multiplikation mit der Testfunktion
2. Integration über das Rechengebiet
3. Äquivalenz zur starken Form
Interpolationsfunktion

Darstellung:
- stückweise linear
- stückweise quadratisch
- stückweise linear (unstetig)
- stückweise konstant
Galerkin-Methode
Gemäß der Galerkin Methode werden die Testfunktionen gleich den Interpolationsfunktionen gesetzt:
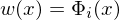
Die Testfunktionen sorgen dafür, dass wir in unserem
Gleichungssystem genügend Gleichungen zur Verfügung haben.
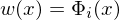
Die Testfunktionen sorgen dafür, dass wir in unserem
Gleichungssystem genügend Gleichungen zur Verfügung haben.
- Qualität der Approximation hängt von Basis- und Testfunktion ab
- Bei Dirichlet-RB treten keine Randterme auf, da
 und
und 
Finite Volumen
- Lösung basiert auf dem Erhaltungssatz

- erster Term des Erhaltungssatzes entspricht dem Volumenintegral
- Berechnung der Flüsse über die Volumenränder entspricht den zweiten und dritten Termen im Erhaltungssatz (Flüsse werden mit FD rekonstruiert)
Vereinfachung des Volumenintegrals
Vereinfachung zeitlicher Term: Volumenmittelung

Approx. der Fluss-Terme:

Approx. der Fluss-Terme:
- über die Volumenränder
- Mittelung an den Rändern
- Upwinding
Explizite vs. implizite Methoden
- Explizite Methoden sind einfacher, aber nur bedingt stabil
- Beschränkung der Zeitschrittweite für Euler-Vorwärts Diskretisierung
- Von Neumann Zahl r beschränkt die Ausbreitung in einem Zeitschritt!
- Implizite Methoden stabil, aber erfordern die Lösung eines Matrix-Systems
Randbedingungen
Dirichlet-RB: geben Werte der Variablen am Rand des betrachteten Gebiets vor (Werte der Knoten am Rand)
Neumann-RB: geben Werte der Ableitungen der Variable am Rand des betrachteten Gebiets vor (Flüsse)
Neumann-RB: geben Werte der Ableitungen der Variable am Rand des betrachteten Gebiets vor (Flüsse)
FD, FE, FV am Beispiel der 2D-Wärmeleitung
FD: Rückwärts-Euler produziert penta-diagonales System
FE: Interpolation auf Dreiecks- oder Viereckselementen
FV: Flüsse werden über Kanten um die Knoten herum berechnet
FE: Interpolation auf Dreiecks- oder Viereckselementen
FV: Flüsse werden über Kanten um die Knoten herum berechnet
Gittertypen
Strukturierte Gitter:
Unstrukturierte Gitter: (Verwendung in Realität)
- Regelmäßige Konnektivität: Anzahl benachbarter Knoten konstant
- In 2D ist der zugehörige Elementtyp ein Rechteck
- weniger Speicherbedarf
- Zelldichte schwer anpassbar
- für einfache Gebiete leicht zu erzeugen
Unstrukturierte Gitter: (Verwendung in Realität)
- Unregelmäßige Konnektivität: Anzahl benachbarter Knoten variabel
- In 2D ist der zugehörige Elementtyp z.B. ein Dreieck
- höherer Speicherbedarf
- Zelldichte leicht anpassbar
- gleicher Generierungsaufwand, unabhängig vom Gebiet (automatisch)
Elementweise Berechnung der Systemmatrix
Assemblierung: In der FE-Methode werden Matrizen elementweise berechnet und dann zur globalen Systemmatrix zusammengesetzt
- Auswertung der Elementmatrix durch numerische Integration (Gauß-Quadratur)
isoparametrische Prinzip
- Transformation von lokalen in globale Koordinaten
- Die Geometrie wird mit denselben Interpolationsfunktionen interpoliert, wie die gesuchte Funktion
- Determinante der Jacobi-Matrix der Transformation lässt sich aus der isoparametrischen Abbildung berechnen
Finite-Elemente-Methode
- Das Problem wird in die schwache Form umformuliert
- Generierung des Rechengitters
- Definition der Interpolationsfunktionen
- elementweise Berechnung von Matrizen: Galerkin, Hutfunktion (Interpolationsfunktion)
- Transformation der Integrationsgebiete auf Referenzgebiete
- Assemblierung der Elementmatrizen zur globalen Matrix
- numerische Integration mittels Gaußquadratur
Voraussetzungen für die Anwendung der FDM, FEM, FVM
- Anfangs- und Randbedingungen: Dirichlet, Neumann
- gegebener Zeitpunkt
Fehlerarten
Modellierungsfehler:
mathematisches Modell nicht angemessen bzw. zu stark vereinfacht, falsche Annahmen oder ein falsches Modell
Interpolationsfehler:
Diskretisierungsfehler:
mathematisches Modell nicht angemessen bzw. zu stark vereinfacht, falsche Annahmen oder ein falsches Modell
Interpolationsfehler:
- numerische Lösung auf kleine Menge zulässiger Lösungen beschränkt, unzureichende Gitterauflösung
- Differenz zwischen der exakten Lösung und ihrer Interpolante
Diskretisierungsfehler:
- Diskretisierung (FD, FE, FV) kann größere Fehler als den Interpolationsfehler einführen, enthält den Interpolationsfehler
- Diskretisierungsfehler e ist die Differenz zwischen der exakten Lösung und der diskreten Lösung
Beispiele für Modellierungsfehler
- Nutzung eines 2D- anstatt eines 3D-Modells
- Modellierung einer inkompressiblen Strömung mit einem Modell für kompressible Strömungen
- Berechnung der Strömung um einen starren statt um einen elastischen Flügels
Interpolationsfehler
- Die Interpolante kann als die beste diskrete Lösung betrachtet werden
- Per Definition ist der Interpolationsfehler an den Knoten Null
- Abhängig von der Gitterschrittweite (je kleiner, desto geringer wird der Interpolationsfehler), Ordnung der Interpolation (höher = besser) (gilt auch für Diskretisierungsfehler)
- Interpolante aus Ansatzfunktionen: stückweise linear, stückweise quadratisch, unstetig stückweise linear, stückweise konstant
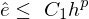
Konvergenz
diskrete Lösung nähert sich analytischer Lösung mit 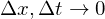
Satz von Lax: Konsistenz und Stabilität bedeuten Konvergenz!
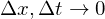
Satz von Lax: Konsistenz und Stabilität bedeuten Konvergenz!
Konsistenz
- Wird die analytische Lösung der Differentialgleichung an den Gitterpunkten ausgewertet und in das diskrete Verfahren eingesetzt, ist die diskrete Gleichung oft nicht erfüllt
- konsistent, wenn diese Abweichung in einer Grenzwertanalyse verschwindet
- diskreter Operator
 nähert sich
nähert sich  mit
mit 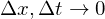

Upwinding
- Verwendung der Rückwärts-Differenzen wird Upwinding genannt: die Ableitung wird nur mit Hilfe der Nachbarwerte stromauf im Sinne der Advektions-Richtung berechnet
- Upwinding fügt dem diskreten System, welches unter den Effekten von negativer numerischer Diffusion leidet, künstliche Diffusion hinzu
Herausforderungen von Advektion
- Advektion stellt eine Herausforderung für numerische Methoden dar
- zentrale Differenzen führen negative numerische Diffusion ein; numerische Lösung zeigt unphysikalische Oszillationen
- Upwinding fügt zu viel künstliche Diffusion hinzu; numerische Lösung zeigt nun unphysikalische Verschmierung
- Optimale Upwinding notwendig bei FD, FE und FV
Zweite Ableitung der Wärmeleitungsgleichung
- die Änderungsrate von T an einem beliebigen Punkt im Stab ist proportional zur zweiten Ortsableitung von T
- Die Proportionalitätskonstante ist eine physikalische Materialeigenschaft und heißt Temperaturleitfähigkeit
- gibt an, wie schnell sich Temperaturänderungen im Stab ausbreiten
Ansatzfunktionen
- Interpolationsfunktionen werden im Finite-Elemente-Kontext als Ansatzfunktionen bezeichnet
- z.B. Hutfunktion, Galerkin
- je höher die Ordnung, desto genauer die Lösung
Warum löst man pDGL über Diskretisierung?
Analytische Lösung oft nicht bekannt, numerische Lösung kann angenähert werden
Finite Elemente anhand einer Zeichnung (Strichmännchen, Tisch)
Vorgehen:
1. System (Gleichungen) aufstellen
2. Randbedingungen einsetzen (Dirichlet, Neumann)
3. Passendes Gitter wählen
1. System (Gleichungen) aufstellen
2. Randbedingungen einsetzen (Dirichlet, Neumann)
3. Passendes Gitter wählen
Kartensatzinfo:
Autor: CoboCards-User
Oberthema: Simulationstechnik RWTH
Thema: CATS
Veröffentlicht: 25.05.2018
Schlagwörter Karten:
Alle Karten (46)
keine Schlagwörter















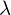 : Wärmeleitfähigkeit
: Wärmeleitfähigkeit