Einsetzungsmethode=
besteht darin, dass man aus einer der beiden Gleichungen eine der Variablen ausrechnet und diesen Ausdruck an Stelle dieser Unbekannten in die andere Gleichung einsetzt
Gleichsetzungsmethode=
besteht darin, dass man aus beiden Gleichungen eine und die selbe Variable freirechnet und die so gefundenen Werte einander gleichsetzt
Additions- und Subtraktionsmethode=
will mann die Koffizienten von y gleichnamig machen, so multipliziert man die erste Gleichung mit dem Faktor von y in der zweiten Gleichung und die zweite Gleichung mit dem Faktor von y in der ersten Gleichung
Addiert man die beiden Gleichungen miteinander, so bekommt man eine Gleichung, die nach x umgestellt werden kann
dann verläuft das ganze nach x, so dass man nach y umstellen kann
Addiert man die beiden Gleichungen miteinander, so bekommt man eine Gleichung, die nach x umgestellt werden kann
dann verläuft das ganze nach x, so dass man nach y umstellen kann
Determinantenverfahren=
die Differenz ad - bc wird als Determinante bezeichnet und in quadratischer Anordnung geschrieben
ad - bc =
Ersetzt man nun die Determinante a und c durch e und f, so erhält man
 = ed - bf
= ed - bf
also den Zähler der x-Komponente der allgemeinen Lösung. Genauso erhält man den Zähler der y-Komponente, nur dass man nun b und d durch e und f ersetzt.
Man bildet zunächst die Hauptdeterminante:
D = \begin{vmatrix} a & b \\ c & d \end{vmatrix}
danach:
 =
=
und
 =
= 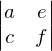
ist D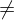 0, so lautet die Lösung:
0, so lautet die Lösung:
 / D |
/ D |  / D
/ D
ad - bc =

Ersetzt man nun die Determinante a und c durch e und f, so erhält man
 = ed - bf
= ed - bfalso den Zähler der x-Komponente der allgemeinen Lösung. Genauso erhält man den Zähler der y-Komponente, nur dass man nun b und d durch e und f ersetzt.
Man bildet zunächst die Hauptdeterminante:
D = \begin{vmatrix} a & b \\ c & d \end{vmatrix}
danach:
 =
=
und
 =
= 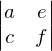
ist D
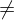 0, so lautet die Lösung:
0, so lautet die Lösung: / D |
/ D |  / D
/ DKartensatzinfo:
Autor: rosa11182
Oberthema: Mathematik
Thema: Algebra
Veröffentlicht: 28.07.2010
Schlagwörter Karten:
Alle Karten (5)
keine Schlagwörter



