This flashcard is just one of a free flashcard set. See all flashcards!
9
Leiten Sie die Epipolarbedingung her.
(Herleitung der E-Matrix)
Mit Translation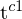
und Rotation 
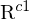wird 
in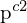 
überführt (Kam1 in Kam2)
1.
2.
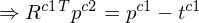
Koplanaritätsbedingung (
auf einer Ebene (Epipolarebene)).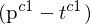 
ist deshalb orthogonal zur Normale 
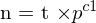der Epipolarebene.
Dies kann durch das Skalarprodukt (entspricht Matrixmultiplikation mit Vektoren (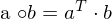
) ausgedrückt werden:
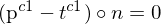=> Die Normale definiert die Epipolarebene.
3.
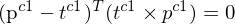
Dadurch werden alle Vektoren in Bezug zueinander gebracht und es wird bewiesen, dass sich alle (3) Vektoren in einer Ebene befinden.
4. Substitution: 2. in 3.
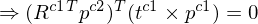
5. Kreuzprodukt als Kreuzproduktmatrix: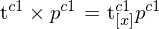
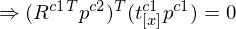
6. Anwendung Matrix-Arithmetrik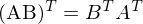
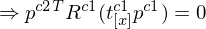
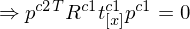
7. Substitution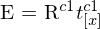
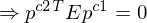
8. Perspektivische Projektion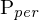
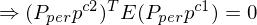
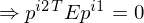
9. wir befinden uns nun in Bildkoordinaten ...das Kreuzprodukt zwischen zwei Punkten in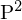
ergibt eine Linie (Projektive Linie (die Epipolarlinie)) => der Schnitt der Bildebene mit der Epipolarebene
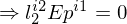
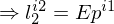
und
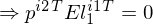
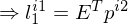
Mit Translation
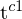und Rotation 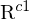wird in 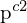überführt (Kam1 in Kam2)1.
2.
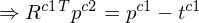
Koplanaritätsbedingung (
auf einer Ebene (Epipolarebene)). 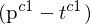ist deshalb orthogonal zur Normale 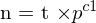der Epipolarebene.Dies kann durch das Skalarprodukt (entspricht Matrixmultiplikation mit Vektoren (
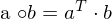) ausgedrückt werden: 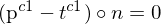=> Die Normale definiert die Epipolarebene. 3.
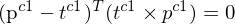
Dadurch werden alle Vektoren in Bezug zueinander gebracht und es wird bewiesen, dass sich alle (3) Vektoren in einer Ebene befinden.
4. Substitution: 2. in 3.
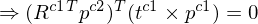
5. Kreuzprodukt als Kreuzproduktmatrix:
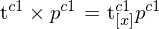
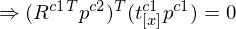
6. Anwendung Matrix-Arithmetrik
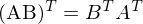
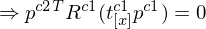
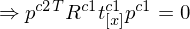
7. Substitution
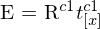
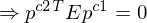
8. Perspektivische Projektion
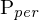
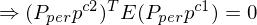
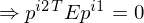
9. wir befinden uns nun in Bildkoordinaten ...das Kreuzprodukt zwischen zwei Punkten in
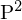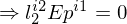
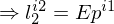
ergibt eine Linie (Projektive Linie (die Epipolarlinie)) => der Schnitt der Bildebene mit der Epipolarebeneund
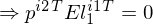
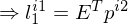
Flashcard info:
Author: CoboCards-User
Main topic: Rechnsersehen
Topic: Epipolargeometrie
Published: 05.11.2010