This flashcard is just one of a free flashcard set. See all flashcards!
13
How are Light Fields parametrized? How can we generate such a parametrization from a set of input images?
Two-Plane Parametrization
Assuming the scene is contained between two parallel planes, the camera plane and the object plane, we can parametrize each ray by a point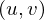 on the camera plane and a point
on the camera plane and a point 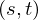 on the object plane. The radiance along that ray is given by
on the object plane. The radiance along that ray is given by
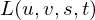
Light Field Generation
1. Re-projection / Rectification of input images
2. Re-binning to produce uniform sampling on camera and object plane
Rectification
Each input image was taken at a camera position with a projection matrix
with a projection matrix 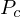 projecting a point
projecting a point  to a point
to a point 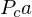 on the camera plane.
on the camera plane.
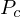 is a transformation from 3D homogenous coordinates to 2D homogenous coordinates. Thus,
is a transformation from 3D homogenous coordinates to 2D homogenous coordinates. Thus,
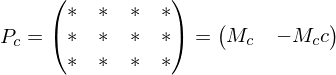
We want to project from the same camera position
from the same camera position  onto a different projection plane given by another projection matrix
onto a different projection plane given by another projection matrix 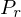 which has the same layout as
which has the same layout as 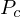
Since the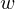 coordinate of
coordinate of  is 1, we can write
is 1, we can write
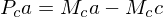
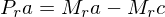
We now multiply the first equation by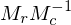 on both sides:
on both sides:
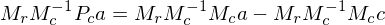
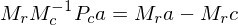
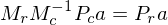
Thus, we can transform projected points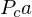 from the input image into projected points of the output image
from the input image into projected points of the output image 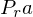 by applying the
by applying the 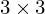 homography
homography
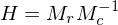
Re-Binning
When rectifying several images from different viewpoints, we obtain an uneven sampling on the camera / object plane. We get a uniform sampling by discretizing the light field and applying the Pull-Push algorithm to provide a color value for every pixel.
Pull-Push algorithm
Explained in 2D here. For Light Fields, we need to do this in 4D. Given: 2D grid of cells and unevenly distributed color samples which are assigned to cells
which are assigned to cells 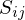 .
.
For each cell, store a color value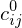 and a weight
and a weight 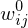 .
.
Initialization
For each cell, compute an average color and an initial weight
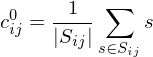
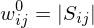
Pull
Average colors and sum weights onto higher levels
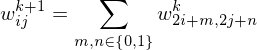
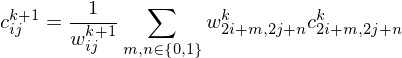
Push
For each cell on the base level, walk up the hierarchy until a cell with weight > 0 is found. Use the color of that cell.
Assuming the scene is contained between two parallel planes, the camera plane and the object plane, we can parametrize each ray by a point
 on the camera plane and a point
on the camera plane and a point 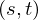 on the object plane. The radiance along that ray is given by
on the object plane. The radiance along that ray is given by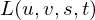
Light Field Generation
1. Re-projection / Rectification of input images
2. Re-binning to produce uniform sampling on camera and object plane
Rectification
Each input image was taken at a camera position
 with a projection matrix
with a projection matrix 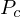 projecting a point
projecting a point  to a point
to a point 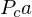 on the camera plane.
on the camera plane.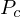 is a transformation from 3D homogenous coordinates to 2D homogenous coordinates. Thus,
is a transformation from 3D homogenous coordinates to 2D homogenous coordinates. Thus,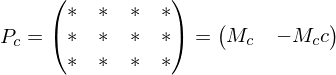
We want to project
 from the same camera position
from the same camera position  onto a different projection plane given by another projection matrix
onto a different projection plane given by another projection matrix 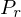 which has the same layout as
which has the same layout as 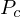
Since the
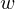 coordinate of
coordinate of  is 1, we can write
is 1, we can write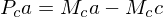
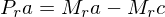
We now multiply the first equation by
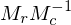 on both sides:
on both sides: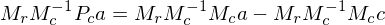
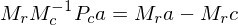
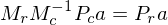
Thus, we can transform projected points
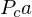 from the input image into projected points of the output image
from the input image into projected points of the output image 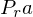 by applying the
by applying the 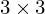 homography
homography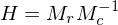
Re-Binning
When rectifying several images from different viewpoints, we obtain an uneven sampling on the camera / object plane. We get a uniform sampling by discretizing the light field and applying the Pull-Push algorithm to provide a color value for every pixel.
Pull-Push algorithm
Explained in 2D here. For Light Fields, we need to do this in 4D. Given: 2D grid of cells and unevenly distributed color samples
 which are assigned to cells
which are assigned to cells 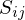 .
.For each cell, store a color value
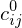 and a weight
and a weight 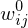 .
.Initialization
For each cell, compute an average color and an initial weight
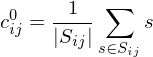
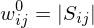
Pull
Average colors and sum weights onto higher levels
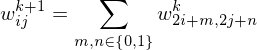
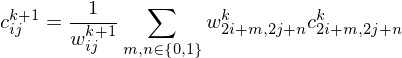
Push
For each cell on the base level, walk up the hierarchy until a cell with weight > 0 is found. Use the color of that cell.
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

