This flashcard is just one of a free flashcard set. See all flashcards!
46
Explain volumetric approaches for extracting a surface from a point cloud!
General idea:
Tangent Plane Estimation
Given a local cloud of points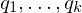 , we want to find a least-squares regression plane
, we want to find a least-squares regression plane
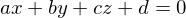
or, for more points:
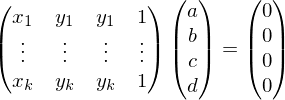
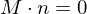
For a least-squares solution, we compute
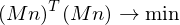
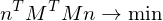
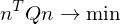
with
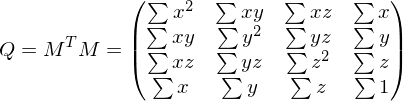
If we shift all points into the center of gravity, this becomes
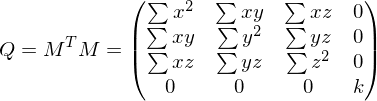
Since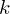 is constant, we can focus on the upper left
is constant, we can focus on the upper left 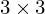 block
block  of
of 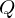 .
.
Find:
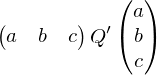
such that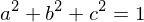 .
.
Find smallest eigenvalue of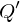 . Scale corresponding eigenvector to
. Scale corresponding eigenvector to 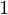 .
.
Consistent Normal Orientation
Construct minimal spanning tree between all points with an edge weight
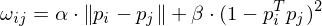
where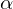 controls how points are penalized for being further away from each other, and
controls how points are penalized for being further away from each other, and 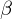 controls how points are penalized for having non-parallel normal directions.
controls how points are penalized for having non-parallel normal directions.
Start at one point where the normal direction is known, e.g. the point with the lowest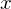 coordinate. From there, walk over the spanning tree and flip normals to make them consistent.
coordinate. From there, walk over the spanning tree and flip normals to make them consistent.
Signed Distance Field Estimation
Impose a voxel grid on the input points. For each grid vertex, estimate the value of a signed distance function for the object.
For every voxel, consider some neighboring samples and compute a weighted average of the distance of the voxel center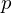 to the respective tangent planes:
to the respective tangent planes:
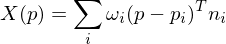
Iso-Surface Extraction
Using Marching Cubes. Output is a watertight two-manifold mesh.
- Estimate tangent planes from point cloud
- Consistently orient normals
- Construct signed distance field from point / normal samples
- Extract iso-surface mesh
Tangent Plane Estimation
Given a local cloud of points
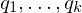 , we want to find a least-squares regression plane
, we want to find a least-squares regression plane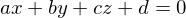
or, for more points:
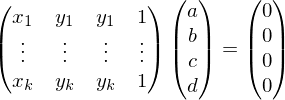
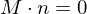
For a least-squares solution, we compute
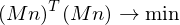
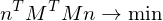
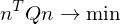
with
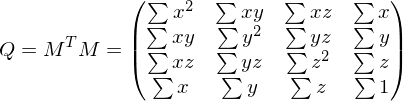
If we shift all points into the center of gravity, this becomes
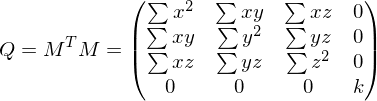
Since
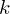 is constant, we can focus on the upper left
is constant, we can focus on the upper left 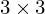 block
block 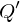 of
of 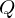 .
.Find:
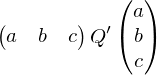
such that
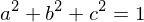 .
.Find smallest eigenvalue of
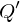 . Scale corresponding eigenvector to
. Scale corresponding eigenvector to 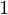 .
.Consistent Normal Orientation
Construct minimal spanning tree between all points with an edge weight
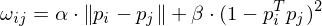
where
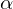 controls how points are penalized for being further away from each other, and
controls how points are penalized for being further away from each other, and 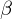 controls how points are penalized for having non-parallel normal directions.
controls how points are penalized for having non-parallel normal directions.Start at one point where the normal direction is known, e.g. the point with the lowest
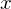 coordinate. From there, walk over the spanning tree and flip normals to make them consistent.
coordinate. From there, walk over the spanning tree and flip normals to make them consistent.Signed Distance Field Estimation
Impose a voxel grid on the input points. For each grid vertex, estimate the value of a signed distance function for the object.
For every voxel, consider some neighboring samples and compute a weighted average of the distance of the voxel center
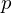 to the respective tangent planes:
to the respective tangent planes: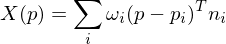
Iso-Surface Extraction
Using Marching Cubes. Output is a watertight two-manifold mesh.
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

