This flashcard is just one of a free flashcard set. See all flashcards!
52
How to compute a Discrete Harmonic Parametrization? Give three examples for weights!
Given a mesh with disk topology of points 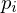 in the mesh domain
in the mesh domain 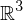 , find points
, find points 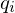 in the parameter domain
in the parameter domain 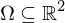 .
.
A function is harmonic if its Laplace is zero, i.e.
is harmonic if its Laplace is zero, i.e.
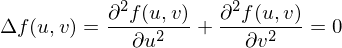
Use a spring model: Edges of the mesh are mapped to springs. Fix parameters of mesh boundary points. Relax remaining points to equilibrium by solving
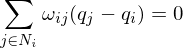
i.e.
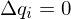
Solve two linear systems:
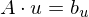
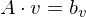
To satisfy Tutte's theorem (and thus ensure a valid parametrization), use a concave boundary shape (circle, square) and have only positive spring weights.
Uniform Weights
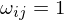
Distributes vertices regularly in the parameter domain. No mesh structure is considered. Strong length and angular distortion.
Chordal Weights
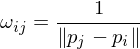
Considers vertex distances. Low length distortion, but angular distortion is not controlled and thus high.
Cotangent Weights
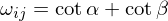
In practice, low length and angular distortion. However, can lead to negative weights (violating Tutte's theorem).
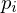 in the mesh domain
in the mesh domain 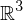 , find points
, find points 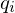 in the parameter domain
in the parameter domain 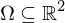 .
.A function
 is harmonic if its Laplace is zero, i.e.
is harmonic if its Laplace is zero, i.e.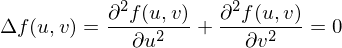
Use a spring model: Edges of the mesh are mapped to springs. Fix parameters of mesh boundary points. Relax remaining points to equilibrium by solving
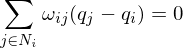
i.e.
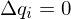
Solve two linear systems:
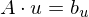
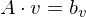
To satisfy Tutte's theorem (and thus ensure a valid parametrization), use a concave boundary shape (circle, square) and have only positive spring weights.
Uniform Weights
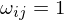
Distributes vertices regularly in the parameter domain. No mesh structure is considered. Strong length and angular distortion.
Chordal Weights
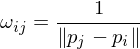
Considers vertex distances. Low length distortion, but angular distortion is not controlled and thus high.
Cotangent Weights
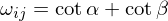
In practice, low length and angular distortion. However, can lead to negative weights (violating Tutte's theorem).
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

