This flashcard is just one of a free flashcard set. See all flashcards!
56
Beweis: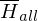 
ist nicht rekursiv aufzählbar
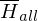ist nicht rekursiv aufzählbarReduziere eine nicht rek. aufz. Sprache auf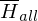 
:
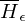nicht rek. aufz. => 
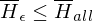bzw. äquivalent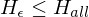 
Konstruiere eine berechenbare Funktion f, die alle Ja/Nein-Instanzen von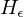
auf alle Ja/Nein-Instanzen von 
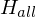abbildet.
w Eingabe für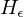
1.) Wenn w keine gültige GN, dann f(w)=w
2.) Wenn w=<M> GN einer TM, dann sei f(w) GN einer TM M* mit folgender Eigenschaft: M* ignoriert die Eingabe und simuliert M auf Eingabe
f ist offensichtlich berechenbar. Falls w keine GN ist, so gilt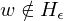
und 
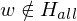
Für w=<M> ist f(w)=<M*>:
|
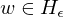=> M hält auf Eingabe
=> M* hält auf jeder Eingabe
=> f(w)=<M*>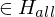
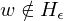
=> M hält nicht auf Eingabe
=> M* hält auf keiner Eingabe
=> f(w)=<M*>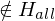
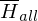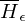: nicht rek. aufz. => 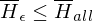bzw. äquivalent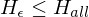 Konstruiere eine berechenbare Funktion f, die alle Ja/Nein-Instanzen von
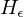auf alle Ja/Nein-Instanzen von 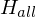abbildet.w Eingabe für
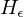
1.) Wenn w keine gültige GN, dann f(w)=w
2.) Wenn w=<M> GN einer TM, dann sei f(w) GN einer TM M* mit folgender Eigenschaft: M* ignoriert die Eingabe und simuliert M auf Eingabe
f ist offensichtlich berechenbar. Falls w keine GN ist, so gilt
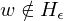und 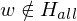Für w=<M> ist f(w)=<M*>:
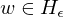|=> M hält auf Eingabe
=> M* hält auf jeder Eingabe
=> f(w)=<M*>
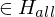
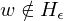
=> M hält nicht auf Eingabe
=> M* hält auf keiner Eingabe
=> f(w)=<M*>
