This flashcard is just one of a free flashcard set. See all flashcards!
24
Was ist eine bijektive Funktion? Welche besondere Eigenschaft hat sie?
Eine Funktion f: 
heißt bijektiv, falls sie injektiv und surjektiv ist.
Mit anderen Worten: auf jedes Element im Wertebereich zeigt genau ein Pfeil, d.h., es gibt eine eins-zu-eins-Zuordnung zwischen den Elementen des Definitionsbereichs und des Wertebereichs.
Die bijektiven Funktionen sind genau die invertierbaren
Funktionen. Zu einer bijektiven Funktion f :
gibt es eine Umkehrfunktion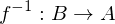 
mit folgenden Eigenschaften:
(
(a)) = a für alle a 
A
(b)) = b für alle b B
heißt bijektiv, falls sie injektiv und surjektiv ist.Mit anderen Worten: auf jedes Element im Wertebereich zeigt genau ein Pfeil, d.h., es gibt eine eins-zu-eins-Zuordnung zwischen den Elementen des Definitionsbereichs und des Wertebereichs.
Die bijektiven Funktionen sind genau die invertierbaren
Funktionen. Zu einer bijektiven Funktion f :
gibt es eine Umkehrfunktion 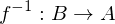mit folgenden Eigenschaften:( (a)) = a für alle a A(b)) = b für alle b BTags: Funktionen, Relationen
Source: VL 2
Source: VL 2
Flashcard info:
Author: P-H-I-L
Main topic: Mathematik
Topic: Mathematische Strukturen
Published: 13.04.2010