This flashcard is just one of a free flashcard set. See all flashcards!
33
How to register two patches obtained by a laser scanner using the Iterative Closest Point algorithm?
Assumption: Scanned patches have identical scale.
Goal: Find a rigid transformation (rotation and translation) for one of the patches to align it with the other.
Algorithm Overview
1. Initial alignment: Provided by the user
2. Matching: Find corresponding points in the two patches
3. Registration: Compute optimal translation and rotation
4. Repeat from step 2 until convergence.
Matching
Matching Strategy: Nearest Neighbor
For every vertex in patch
in patch 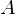 , select the nearest neighbor vertex
, select the nearest neighbor vertex  from patch
from patch 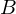 .
.
Filtering: Remove those matchings where one vertex is a boundary vertex (since boundary vertices match to many points). Remove matchings with a high distance. Remove matchings with a high normal deviation.
Matching Strategy: Normal Piercing
From each vertex in patch
in patch 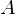 , shoot a ray into normal direction. If this ray intersects with
, shoot a ray into normal direction. If this ray intersects with 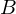 in point
in point  , add the correspondence
, add the correspondence 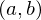 .
.
Registration
Given a list of corresponding vertices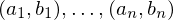
we want to find a transformation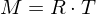 such that
such that
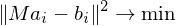
Finding the translational part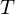 just amounts to shifting the center of gravity of the
just amounts to shifting the center of gravity of the 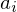 into that of the
into that of the 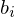 by adding an offset
by adding an offset
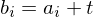
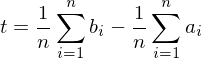
We just assume this translational registration has already taken place and just focus on the rotational alignment:
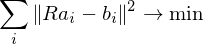
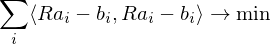

The first and last term are independent of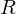
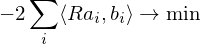
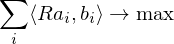
Problem: Finding a solution for the rotation matrix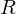 requires finding 9 unknowns (of which 6 need to be constrained). Solution: Formulate the rotation as a quaternion (gives 4 unknowns with 1 additional constraint).
requires finding 9 unknowns (of which 6 need to be constrained). Solution: Formulate the rotation as a quaternion (gives 4 unknowns with 1 additional constraint).
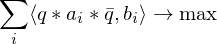
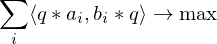
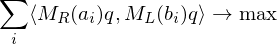
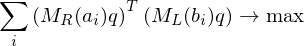
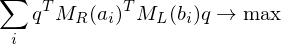
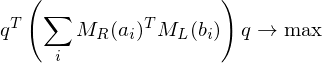
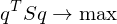
 is a symmetric matrix. To compute a solution for
is a symmetric matrix. To compute a solution for 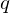 , find the eigenvector to the largest eigenvalue. Normalize to obtain a rotation.
, find the eigenvector to the largest eigenvalue. Normalize to obtain a rotation.
Goal: Find a rigid transformation (rotation and translation) for one of the patches to align it with the other.
Algorithm Overview
1. Initial alignment: Provided by the user
2. Matching: Find corresponding points in the two patches
3. Registration: Compute optimal translation and rotation
4. Repeat from step 2 until convergence.
Matching
Matching Strategy: Nearest Neighbor
For every vertex
 in patch
in patch  , select the nearest neighbor vertex
, select the nearest neighbor vertex  from patch
from patch 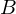 .
.Filtering: Remove those matchings where one vertex is a boundary vertex (since boundary vertices match to many points). Remove matchings with a high distance. Remove matchings with a high normal deviation.
Matching Strategy: Normal Piercing
From each vertex
 in patch
in patch 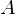 , shoot a ray into normal direction. If this ray intersects with
, shoot a ray into normal direction. If this ray intersects with 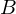 in point
in point  , add the correspondence
, add the correspondence 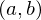 .
.Registration
Given a list of corresponding vertices
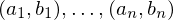
we want to find a transformation
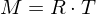 such that
such that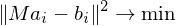
Finding the translational part
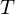 just amounts to shifting the center of gravity of the
just amounts to shifting the center of gravity of the 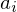 into that of the
into that of the 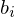 by adding an offset
by adding an offset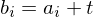
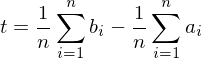
We just assume this translational registration has already taken place and just focus on the rotational alignment:
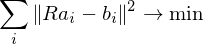
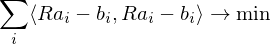

The first and last term are independent of
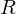
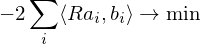
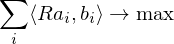
Problem: Finding a solution for the rotation matrix
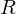 requires finding 9 unknowns (of which 6 need to be constrained). Solution: Formulate the rotation as a quaternion (gives 4 unknowns with 1 additional constraint).
requires finding 9 unknowns (of which 6 need to be constrained). Solution: Formulate the rotation as a quaternion (gives 4 unknowns with 1 additional constraint).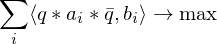
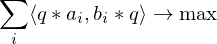
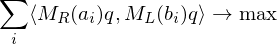
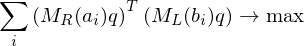
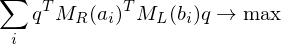
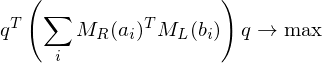
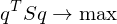
 is a symmetric matrix. To compute a solution for
is a symmetric matrix. To compute a solution for 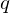 , find the eigenvector to the largest eigenvalue. Normalize to obtain a rotation.
, find the eigenvector to the largest eigenvalue. Normalize to obtain a rotation.Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

