This flashcard is just one of a free flashcard set. See all flashcards!
45
Explain Contour Tessellation using Voronoi Filtering!
Given: Point cloud of an object. Goal: Triangulation of the surface.
In 2D: We observe that the medial axis of a shape cuts through its interior (or, more general, through concave regions). The idea is to let the medial axis cut away interior edges of the Delaunay triangulation of the shape.
Another observation: The vertices of the Voronoi diagram of the contour points approximate the medial axis.
Strategy: Compute Voronoi vertices and add them to the input vertices. Compute Delaunay triangulation. Remove Voronoi vertices.
In 3D: Problem: Some Voronoi vertices lie not only near the medial axis but also close to the contour. Thus, only keep those Voronoi vertices (called poles) which lie at the innermost or outermost tips of their respective cells.
For each cell, identify one pole vertex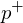 as the farthest vertex from the cell center
as the farthest vertex from the cell center  . For
. For 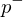 , choose the most distant vertex to
, choose the most distant vertex to 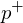 for which
for which  .
.
Voronoi cells of convex hull points are infinitely large. In order to find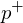 , average the normals of the convex hull triangles at
, average the normals of the convex hull triangles at  and use as
and use as 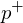 an outward projection along this normal.
an outward projection along this normal.
Like in 2D, add the pole vertices to the input vertices. Tetrahedralize and remove pole vertices (and their incident edges and faces). Some additional cleanup is required to remove non-manifold configurations on the surface.
In 2D: We observe that the medial axis of a shape cuts through its interior (or, more general, through concave regions). The idea is to let the medial axis cut away interior edges of the Delaunay triangulation of the shape.
Another observation: The vertices of the Voronoi diagram of the contour points approximate the medial axis.
Strategy: Compute Voronoi vertices and add them to the input vertices. Compute Delaunay triangulation. Remove Voronoi vertices.
In 3D: Problem: Some Voronoi vertices lie not only near the medial axis but also close to the contour. Thus, only keep those Voronoi vertices (called poles) which lie at the innermost or outermost tips of their respective cells.
For each cell, identify one pole vertex
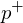 as the farthest vertex from the cell center
as the farthest vertex from the cell center  . For
. For 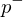 , choose the most distant vertex to
, choose the most distant vertex to 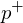 for which
for which  .
.Voronoi cells of convex hull points are infinitely large. In order to find
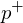 , average the normals of the convex hull triangles at
, average the normals of the convex hull triangles at  and use as
and use as 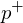 an outward projection along this normal.
an outward projection along this normal.Like in 2D, add the pole vertices to the input vertices. Tetrahedralize and remove pole vertices (and their incident edges and faces). Some additional cleanup is required to remove non-manifold configurations on the surface.
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

