This flashcard is just one of a free flashcard set. See all flashcards!
8
What is the goal of Subdivision techniques? Explain Subdivision using the Lane-Riesenfeld technique!
We interpret a sequence of points 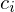 as the control points of a B-Spline curve
as the control points of a B-Spline curve
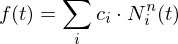
Now, we want to describe the same curve with a higher number of control points.
We define two operators on the sequence
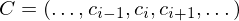
Doubling
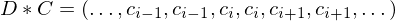
Averaging
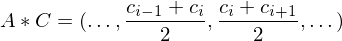
To determine the new vertex positions, we compute weighted positions based on even / odd rules.
Subdivision Operators
Linear (primal)
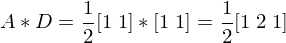
Quadratic Spline (dual)
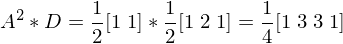
Cubic Spline (primal)
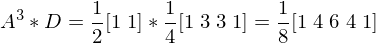
TODO: Fix this explanation
Consider the B-Spline basis function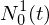 .
.
It is a piecewise linear function between
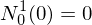
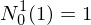
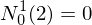
We can write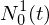 as an affine combination of the same function with parameter
as an affine combination of the same function with parameter  :
:
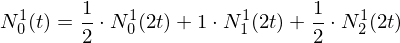
We can do this for uniform B-Spline basis functions in general:
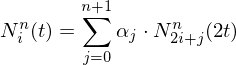
where
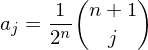
 as the control points of a B-Spline curve
as the control points of a B-Spline curve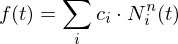
Now, we want to describe the same curve with a higher number of control points.
We define two operators on the sequence
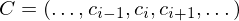
Doubling
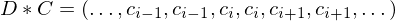
Averaging
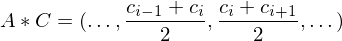
To determine the new vertex positions, we compute weighted positions based on even / odd rules.
Subdivision Operators
Linear (primal)
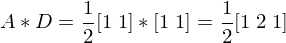
Quadratic Spline (dual)
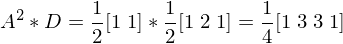
Cubic Spline (primal)
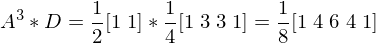
TODO: Fix this explanation
Consider the B-Spline basis function
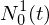 .
.It is a piecewise linear function between
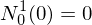
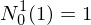
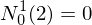
We can write
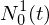 as an affine combination of the same function with parameter
as an affine combination of the same function with parameter 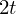 :
: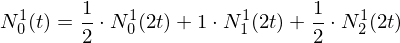
We can do this for uniform B-Spline basis functions in general:
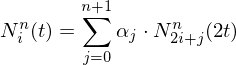
where
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

