This flashcard is just one of a free flashcard set. See all flashcards!
76
LOOP-Programme
ersetze WHILE durch LOOP-Schleife:
LOOP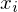
DO P END ( 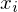darf nicht in P vorkommen!)
=> P wird sooft ausgeführt, wie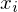 es vorgibt
=> jedes LOOP-Konstrukt kann durch ein WHILE-Konstrukt ersetzt werden, aber nicht umgekehrt
=> LOOP-Programme terminieren immer, da man bei Eintritt in LOOP-Schleife weiß, wie oft diese ausgeführt wird (mit WHILE kann man dagegen Endlosschleifen konstruieren) => nicht alle Funktionen, die auf TM berechenbar sind, sind es auch LOOP-berechenbar
=> LOOP ist nicht TM-mächtig (Möglichkeit der Nicht-Terminierung ausgeschlossen)
Beweis: (berechenbare totale) Funktion gefunden, die von einer TM berechnet werden kann nicht aber durch ein LOOP-Programm:
Ackermann-Funktion
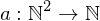
A(0,n) = n+1 für n >=0
A(m+1,0) = A(m,1) für m>=0
A(m+1,n+1) = A(m,A(m+1,n)) für m,n >=0
LOOP
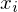DO P END ( 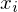darf nicht in P vorkommen!)=> P wird sooft ausgeführt, wie
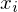es vorgibt=> jedes LOOP-Konstrukt kann durch ein WHILE-Konstrukt ersetzt werden, aber nicht umgekehrt
=> LOOP-Programme terminieren immer, da man bei Eintritt in LOOP-Schleife weiß, wie oft diese ausgeführt wird (mit WHILE kann man dagegen Endlosschleifen konstruieren) => nicht alle Funktionen, die auf TM berechenbar sind, sind es auch LOOP-berechenbar
=> LOOP ist nicht TM-mächtig (Möglichkeit der Nicht-Terminierung ausgeschlossen)
Beweis: (berechenbare totale) Funktion gefunden, die von einer TM berechnet werden kann nicht aber durch ein LOOP-Programm:
Ackermann-Funktion
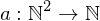
A(0,n) = n+1 für n >=0
A(m+1,0) = A(m,1) für m>=0
A(m+1,n+1) = A(m,A(m+1,n)) für m,n >=0
