This flashcard is just one of a free flashcard set. See all flashcards!
76
Explain the de Casteljau algorithm!
de Casteljau algorithm gives a geometric procedure to construct points on Bézier curves.
Example: Given control points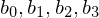 (cubic spline), we compute
(cubic spline), we compute
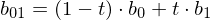
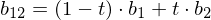
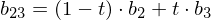
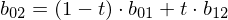
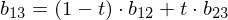
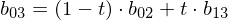
Note how this schema iteratively evaluates the Bernstein polynomials for all coefficients:
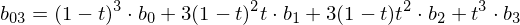
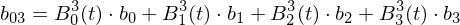
Useful properties:
Example: Given control points
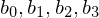 (cubic spline), we compute
(cubic spline), we compute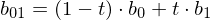
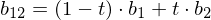
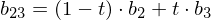
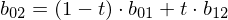
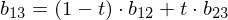
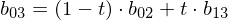
Note how this schema iteratively evaluates the Bernstein polynomials for all coefficients:
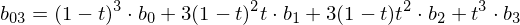
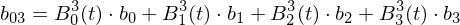
Useful properties:
- Numerically robust: Sequence of affine combinations (instead of sum of scaled polynomial coefficients)
- First derivative:

Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

