This flashcard is just one of a free flashcard set. See all flashcards!
19
Was sind die Ausgabeparameter der Singulärwertzerlegung (SVD)? ... Wie lassen sie sich interpretieren?
Sie ist eine Normalform für Matrizen und zerlegt eine Matrix 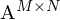 in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.
in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.
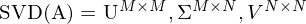
A wieder aus 3 Matrizen zurückrechnen:
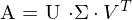
Die Matrix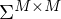 :
:
Enthält auf der Diagonalen, positive, nach der Größe sortierte Singulärwerte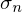 .
.
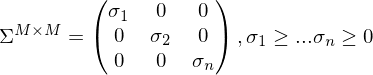
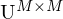 :
:
Die Singulärwerte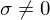 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 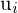 der Matrix U sind die Basisvektoren des Bildraumes.
der Matrix U sind die Basisvektoren des Bildraumes.
Die Spaltenvektoren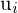 sind die Eigenvektoren von
sind die Eigenvektoren von 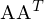 (bei
(bei  => Zeilenvektoren)
=> Zeilenvektoren)
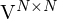 :
:
Die zu den Singulärwerten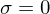 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 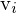 sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei
sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei 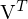 => Zeilenvektoren)
=> Zeilenvektoren)

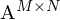 in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.
in 3 einzelne Matrizen mit jeweils speziellen Eigenschaften. Es können die Singulärwerte der Matrix abgelsen werden.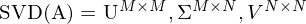
A wieder aus 3 Matrizen zurückrechnen:
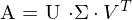
Die Matrix
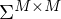 :
:Enthält auf der Diagonalen, positive, nach der Größe sortierte Singulärwerte
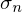 .
.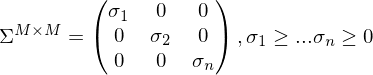
- Rang(A) = Anzahl Singulärwerte
 0
0 - Dimension des Nullraums (Kern) entspricht Anzahl
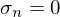
- Singulärwerte sind die Quadratwurzeln der Eigenwerte von
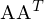
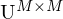 :
:Die Singulärwerte
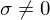 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 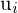 der Matrix U sind die Basisvektoren des Bildraumes.
der Matrix U sind die Basisvektoren des Bildraumes.Die Spaltenvektoren
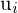 sind die Eigenvektoren von
sind die Eigenvektoren von 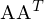 (bei
(bei  => Zeilenvektoren)
=> Zeilenvektoren)-
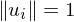
- '
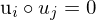
- => sind orthonormal
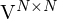 :
:Die zu den Singulärwerten
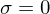 korrespondierenden Spaltenvektoren
korrespondierenden Spaltenvektoren 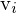 sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei
sind die Basisvektoren des Nullraums. Die Spaltenvektoren sind ebenfalls orthonormal. (bei 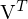 => Zeilenvektoren)
=> Zeilenvektoren)
- Beispiel SVD einer Scherung
-
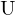 und
und 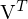 können als Rotationsmatrizen interpretiert werden
können als Rotationsmatrizen interpretiert werden -
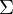 als Skalierungsmatrix um die Faktoren
als Skalierungsmatrix um die Faktoren 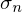
Flashcard info:
Author: CoboCards-User
Main topic: Rechnsersehen
Topic: Epipolargeometrie
Published: 05.11.2010

