This flashcard is just one of a free flashcard set. See all flashcards!
38
Explain Poisson reconstruction in the context of mesh generation!
We assume an underlying characteristic function  that represents the object
that represents the object

By convoluting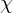 with a smoothing kernel
with a smoothing kernel 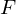 , we obtained a blurred version
, we obtained a blurred version
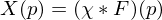
of which the gradient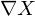 coincides with the normals of the object we want to reconstruct.
coincides with the normals of the object we want to reconstruct.
Given points with estimated normals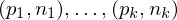 , we can thus state that
, we can thus state that
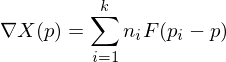
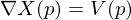
In order to solve for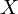 , we turn the problem into a Poisson equation:
, we turn the problem into a Poisson equation:
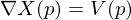
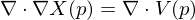
Which can be discretized into a linear system by taking finite differences.
Non-oriented normals
If we only have normal directions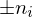 without consistent orientations, we can state that
without consistent orientations, we can state that 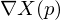 should be parallel to the normal directions:
should be parallel to the normal directions:

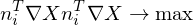

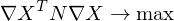
With the additonal smoothness constraint:
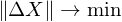
 that represents the object
that represents the object
By convoluting
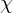 with a smoothing kernel
with a smoothing kernel 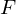 , we obtained a blurred version
, we obtained a blurred version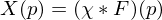
of which the gradient
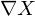 coincides with the normals of the object we want to reconstruct.
coincides with the normals of the object we want to reconstruct.Given points with estimated normals
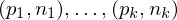 , we can thus state that
, we can thus state that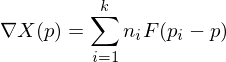
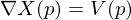
In order to solve for
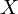 , we turn the problem into a Poisson equation:
, we turn the problem into a Poisson equation: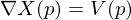
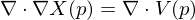
Which can be discretized into a linear system by taking finite differences.
Non-oriented normals
If we only have normal directions
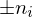 without consistent orientations, we can state that
without consistent orientations, we can state that 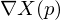 should be parallel to the normal directions:
should be parallel to the normal directions:
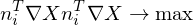

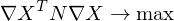
With the additonal smoothness constraint:
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

