This flashcard is just one of a free flashcard set. See all flashcards!
51
Give two definitions of the Voronoi diagram of a point set!
Given: Set of sites 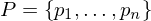
Closest Points
The Voronoi cell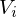 of a site
of a site 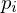 is given by the set of all points which are closer to
is given by the set of all points which are closer to 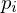 than to any other site
than to any other site 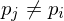 :
:
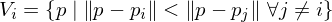
Halfspace Intersection
Each pair of sites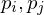 divides the space into a halfspace points which are closer to
divides the space into a halfspace points which are closer to 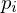 than to
than to 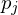
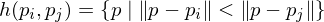
Then,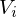 can be described as the intersection of all halfspaces formed with other sites:
can be described as the intersection of all halfspaces formed with other sites:
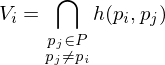
From this definition, it is obvious that all Voronoi cells are convex.
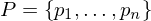
Closest Points
The Voronoi cell
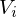 of a site
of a site 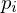 is given by the set of all points which are closer to
is given by the set of all points which are closer to 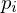 than to any other site
than to any other site 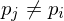 :
: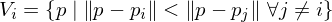
Halfspace Intersection
Each pair of sites
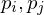 divides the space into a halfspace points which are closer to
divides the space into a halfspace points which are closer to 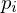 than to
than to 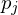
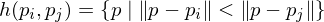
Then,
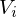 can be described as the intersection of all halfspaces formed with other sites:
can be described as the intersection of all halfspaces formed with other sites: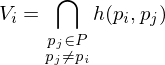
From this definition, it is obvious that all Voronoi cells are convex.
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

