This flashcard is just one of a free flashcard set. See all flashcards!
28
Give a smoothing operator for a curve of vertices in 2D space! What analytical meaning does this operator have? How can we design a better smoothing operator?
Given: Line of vertices 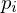
An intuitive smoothing operator is
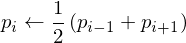
or
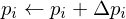
with
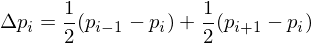
Assuming the points are generated by an arc-length parametrized function
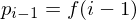
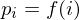
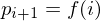
we can approximate the first derivative by divided differences:
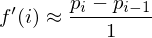
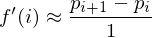
And the second derivative by again taking divided differences:
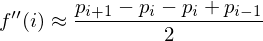
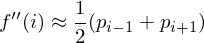
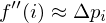
Thus, the smoothing operator approximates the second derivative of the curve.
By writing the points as a matrix
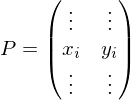
We can write the smoothing operator as a matrix vector product
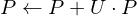
where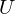 is a sparse matrix with
is a sparse matrix with 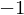 on the main diagonal and
on the main diagonal and  on the two minor diagonals.
on the two minor diagonals.
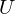 is symmetric. Thus, it has an orthogonal basis of eigenvectors
is symmetric. Thus, it has an orthogonal basis of eigenvectors 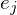 . We can represent
. We can represent 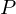 in this basis:
in this basis:
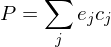
where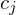 are suitable (two-dimensional) coefficients.
are suitable (two-dimensional) coefficients.
Applying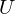 to
to 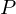 can now be written as
can now be written as
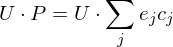
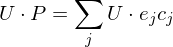
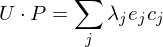
Thus, we can interpret smoothing as a scaling of the eigenvectors of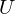 .
.
TODO: Eigenfunctions of U and DFT
Filter Design
Our smoothing operator reduces mid and high frequencies of the mesh. Thus,
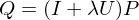
only contains the low frequencies of the input. By subtraction, we get the mid and high frequency parts:
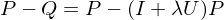
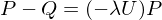
We now apply our smoothing operator only to those mid and high frequencies:
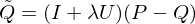
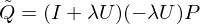
Combining the low and smoothed high frequency terms gives:
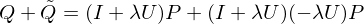
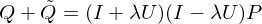
Which is a smoothing operator which only dampens the mid and high frequencies.
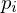
An intuitive smoothing operator is
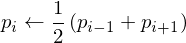
or
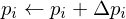
with
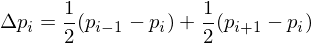
Assuming the points are generated by an arc-length parametrized function
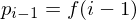
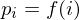
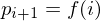
we can approximate the first derivative by divided differences:
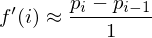
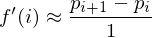
And the second derivative by again taking divided differences:
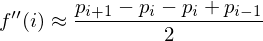
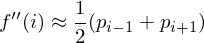
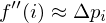
Thus, the smoothing operator approximates the second derivative of the curve.
By writing the points as a matrix
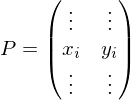
We can write the smoothing operator as a matrix vector product
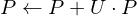
where
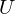 is a sparse matrix with
is a sparse matrix with 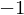 on the main diagonal and
on the main diagonal and  on the two minor diagonals.
on the two minor diagonals.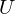 is symmetric. Thus, it has an orthogonal basis of eigenvectors
is symmetric. Thus, it has an orthogonal basis of eigenvectors 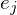 . We can represent
. We can represent 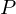 in this basis:
in this basis: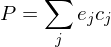
where
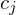 are suitable (two-dimensional) coefficients.
are suitable (two-dimensional) coefficients.Applying
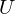 to
to 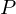 can now be written as
can now be written as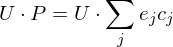
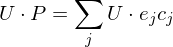
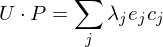
Thus, we can interpret smoothing as a scaling of the eigenvectors of
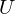 .
.TODO: Eigenfunctions of U and DFT
Filter Design
Our smoothing operator reduces mid and high frequencies of the mesh. Thus,
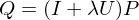
only contains the low frequencies of the input. By subtraction, we get the mid and high frequency parts:
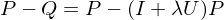
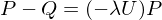
We now apply our smoothing operator only to those mid and high frequencies:
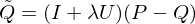
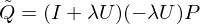
Combining the low and smoothed high frequency terms gives:
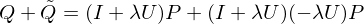
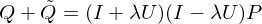
Which is a smoothing operator which only dampens the mid and high frequencies.
Flashcard info:
Author: janisborn
Main topic: Informatik
Topic: Computergrafik
School / Univ.: RWTH Aachen
City: Aachen
Published: 18.05.2022

