Nennen Sie drei wesentliche Nichtlinearitäten bei strukturmechanischen Berechnungen und geben Sie zu jeder ein unterschiedliches Anwendungsbeispiel!
- geometrische Nichtlinearität (große Verzerrungen)
- physikalische Nichtlinearität (Plastifizieren / Kriechen)
- Systemnichtlinearität (Kontakt)
- physikalische Nichtlinearität (Plastifizieren / Kriechen)
- Systemnichtlinearität (Kontakt)
Wie lautet das Gleichungssystem, das bei dynamischen Festigkeitsberechnungen zu lösen ist?
Benennen Sie die Symbole!
Benennen Sie die Symbole!
M * ü + K * u = F(t)
M = globale Massenmatrix
ü = Matrix der Knotenbeschleunigungen
K = globale Steifigkeitsmatrix
u = Matrix der Knotenverschiebungen /-verdrehungen
F(t) = Matrix der äußeren Lasten
M = globale Massenmatrix
ü = Matrix der Knotenbeschleunigungen
K = globale Steifigkeitsmatrix
u = Matrix der Knotenverschiebungen /-verdrehungen
F(t) = Matrix der äußeren Lasten
Wie lautet das Gleichungssystem, das bei transienten Temperaturfeldberechnungen zu lösen ist?
Benennen Sie die Symbole!
Benennen Sie die Symbole!
CT * T' + KT * T = Q
CT = Matrix der speziefischen Wärme
KT = Matrix der Wärmeleitfähigkeit
T = Spaltenmatrix der unbekannten Knotentemperaturen
Q = Wärmestromvektor infolge Konvektion und Strahlung
CT = Matrix der speziefischen Wärme
KT = Matrix der Wärmeleitfähigkeit
T = Spaltenmatrix der unbekannten Knotentemperaturen
Q = Wärmestromvektor infolge Konvektion und Strahlung
Die FE - Methode ist ein Näherungsverfahren. Wie stellen Sie eine ausreichende Genauigkeit der Ergebnisse sicher?
An wichtigen Stellen der Beobachtung wird das Netz stetig verfeinert. Weichen die Änderungen des Spannungs- und Verformungsergebnisses nur gering vom vorangegangenen Ergebnis ab, wird eine gute Genauigkeit erreicht.
Tritt Konvergenz auf, ist eine ausreichende Genauigkeit erreicht.
Tritt Konvergenz auf, ist eine ausreichende Genauigkeit erreicht.
Welchen Einfluss haben der Grad der statischen Unbestimmtheit des Systems und der Grad der Ansatzfunktion des Elementes (linear / quadratisch) auf den Lösungsaufwand und die Genauigkeit?
Grad der statischen Unbestimmtheit:
Grad der Ansatzfunktion:
- je höhergradig unbestimmt, desto weniger Lösungsaufwand
- kein Einfluss auf die Genauigkeit
Grad der Ansatzfunktion:
- Je höhergradig, desto genauer die Ergebnisse
- je höhergradig, desto höher der Lösungsaufwand bei gleichbleibender Netzfeinheit
Was verstehen Sie unter "modaler Superposition"?
Für welche Fragen wird sie angewandt?
Welche anderen Lösungsverfahren sollten wann zum Einsatz kommen?
Für welche Fragen wird sie angewandt?
Welche anderen Lösungsverfahren sollten wann zum Einsatz kommen?
"Modale Superposition" ist ein iteratives Lösungsverfahren. Die Lösungen aus den einzelnen Eigenformen werden überlagert.
Nur für lineare dynamische Probleme.
Explizite Zeitintegration ==> extrem dynamische Probleme (z.B. Crash - Berechnungen)
Implizite Zeitintegration ==> Standardprobleme
Nur für lineare dynamische Probleme.
Explizite Zeitintegration ==> extrem dynamische Probleme (z.B. Crash - Berechnungen)
Implizite Zeitintegration ==> Standardprobleme
Definieren Sie die Begriffe "Membran", "Scheibe", "Schale" und "2D-RVZ"!
Membran:
Biegeschlaffes Flächenelement, das senkrecht zur Fläche belastet werden kann. Anwendungen sind Zelte, Ballone, Membranen.
Scheibe:
Ebenes Element, das nur in seiner Ebene belastet werden kann und keine Biegung erfahren.
Schale:
Allgemeinstes Flächenelement (i. allg. gekrümmte Elemente), das Lasten parallel und senkrecht zur Mittelfläche aufnimmt.
2D - RVZ: (RVZ = rotationssymmetrischer Verzerrungszustand)
2D-Solid mit angewähltem rotationssymmetrischem Verzerrungszustand für rotationssymmetrische Probleme. Statt der Koordinaten x, y und z werden nun r,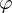 und z verwendet.
und z verwendet.
Biegeschlaffes Flächenelement, das senkrecht zur Fläche belastet werden kann. Anwendungen sind Zelte, Ballone, Membranen.
Scheibe:
Ebenes Element, das nur in seiner Ebene belastet werden kann und keine Biegung erfahren.
Schale:
Allgemeinstes Flächenelement (i. allg. gekrümmte Elemente), das Lasten parallel und senkrecht zur Mittelfläche aufnimmt.
2D - RVZ: (RVZ = rotationssymmetrischer Verzerrungszustand)
2D-Solid mit angewähltem rotationssymmetrischem Verzerrungszustand für rotationssymmetrische Probleme. Statt der Koordinaten x, y und z werden nun r,
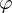 und z verwendet.
und z verwendet.Definieren Sie die Begriffe "Stab", "Balken (allg.)" und "1D-RVZ"!
Stab:
Ein gerades, schlankes Bauteil, das nur Normalkräfte N (Zug/Druck) überträgt. Lasten können nur an den gelenkig gelagerten Stabenden als Axialkräfte eingeleitet werden.
Balken:
Ein gerades, schlankes Bauteil, das quer zur Mittellinie belastet wird. Es treten Querkräfte und Biegemomente auf.
1D - RVZ:
Es bildet einen Meridianschnitt durch eine dünnwandige Struktur mit rotationssymmetrischem Spannungs- und Verzerrungszustand ab.
Ein gerades, schlankes Bauteil, das nur Normalkräfte N (Zug/Druck) überträgt. Lasten können nur an den gelenkig gelagerten Stabenden als Axialkräfte eingeleitet werden.
Balken:
Ein gerades, schlankes Bauteil, das quer zur Mittellinie belastet wird. Es treten Querkräfte und Biegemomente auf.
1D - RVZ:
Es bildet einen Meridianschnitt durch eine dünnwandige Struktur mit rotationssymmetrischem Spannungs- und Verzerrungszustand ab.
Welche Zeitintegrationsverfahren werden zur Lösung dynamischer Probleme angewandt? Nennen Sie die Kriterien für eine sinnvolle Auswahl!
modales Verfahren, implizites Verfahren, explizites Verfahren
1. Auswahlkriterium -> nieder- oder hochfrequente Anregung
2. Auswahlkriterium -> lineares / nichtlineares Problem
hochfrequente Anregung -> explizites Verfahren
niederfrequente Anregung -> implizites oder modales Verfahren
lineares Problem -> implizites oder modales Verfahren
nichtlineares Problem -> implizites Verfahren
1. Auswahlkriterium -> nieder- oder hochfrequente Anregung
2. Auswahlkriterium -> lineares / nichtlineares Problem
hochfrequente Anregung -> explizites Verfahren
niederfrequente Anregung -> implizites oder modales Verfahren
lineares Problem -> implizites oder modales Verfahren
nichtlineares Problem -> implizites Verfahren
Flashcard set info:
Author: CoboCards-User
Main topic: Maschinenbau
Topic: FEM
School / Univ.: FH Aachen
City: Aachen
Published: 08.09.2011
Tags: Prof. Raatschen
Card tags:
All cards (19)
no tags



