1.Was versteht man unter Messunsicherheit?
2. Wie wird die Messunsicherheit quantitativ beschrieben?
3. Welche Möglichkeit besteht, diese Unsicherheit zu
verringern?
2. Wie wird die Messunsicherheit quantitativ beschrieben?
3. Welche Möglichkeit besteht, diese Unsicherheit zu
verringern?
1.
Messunsicherheit:
- zufälligen Fehler aller Einzelvariablen, aus denen das Messergebnis berechnet wird
- unbekannte, weil nicht messbare und daher nur abschätzbare systematische Fehler
=> Systematische und zufällige Fehler
2.
Quantitative Beschreibung:
u kann dabei:
- Vertrauensbereich
- Standardabweichung
- Differenz zwischen zwei Einzelwerten
sein.
3.
Verringerung: Unabhängige Versuche.
Wenn sich eine genügend große Zahl von Laboratorien an einem Ringversuch
beteiligt, bei dem in allen Laboratorien Messungen unter vergleichbaren
Bedingungen durchgeführt werden, dann lassen sich die Standardabweichungen
„innerhalb der Laboratorien“ (Wiederhol- Bedingungen) und „zwischen den
Laboratorien“ (Vergleich-Bedingungen) mit Hilfe einer Varianzanalyse trennen.
=> Varianzanalyse
Messunsicherheit:
- zufälligen Fehler aller Einzelvariablen, aus denen das Messergebnis berechnet wird
- unbekannte, weil nicht messbare und daher nur abschätzbare systematische Fehler
=> Systematische und zufällige Fehler
2.
Quantitative Beschreibung:
u kann dabei:
- Vertrauensbereich
- Standardabweichung
- Differenz zwischen zwei Einzelwerten
sein.
3.
Verringerung: Unabhängige Versuche.
Wenn sich eine genügend große Zahl von Laboratorien an einem Ringversuch
beteiligt, bei dem in allen Laboratorien Messungen unter vergleichbaren
Bedingungen durchgeführt werden, dann lassen sich die Standardabweichungen
„innerhalb der Laboratorien“ (Wiederhol- Bedingungen) und „zwischen den
Laboratorien“ (Vergleich-Bedingungen) mit Hilfe einer Varianzanalyse trennen.
=> Varianzanalyse
Die Verschiebung in einem Finiten Element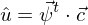 
setzt sich zusammen aus den unnormierten Ansatzfunktionen 
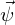und den Koeffizienten 
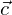. Unter Verwendung der Normierungsmatrix 
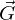lassen sich die Knotenfreiwerte 
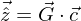bestimmen. Leiten Sie damit die normierten Ansatzfunktionen 
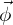her, so dass gilt: 
.
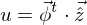Formulieren Sie die Steifigkeitsmatrix für ein Balkenelement
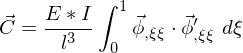
unter Verwendung der unnormierten Ansatzfunktion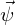
.
Hinweis: Für die Transponierung eines Matrizenproduktes gilt allgemein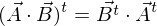
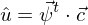setzt sich zusammen aus den unnormierten Ansatzfunktionen 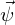und den Koeffizienten 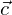. Unter Verwendung der Normierungsmatrix 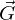lassen sich die Knotenfreiwerte 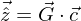bestimmen. Leiten Sie damit die normierten Ansatzfunktionen 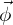her, so dass gilt: 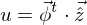.Formulieren Sie die Steifigkeitsmatrix für ein Balkenelement
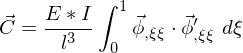
unter Verwendung der unnormierten Ansatzfunktion
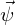.Hinweis: Für die Transponierung eines Matrizenproduktes gilt allgemein
die Steifigkeitsmatrix 
und die Lasspalte 
im globalen Koordinatensystem?
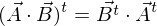
Die Verschiebungen in einem Finiten Element lassen sich einerseits mit unnormierten Ansätzen u=Ψ^T*c und andererseits mit normierten Ansätzen u=Φ^,*c beschreiben. Es gilt der Zusammenhang z^=G*c.
Erläutern Sie die Unterschiede zwischen den beiden Arten von Ansätzen. In welchem Fall werden unnormierte Ansätze verwendet?
Erläutern Sie die Unterschiede zwischen den beiden Arten von Ansätzen. In welchem Fall werden unnormierte Ansätze verwendet?
normierte Ansätze:
Bei diesen Ansätzen sind die Freiwerte physikalisch relevant. Sie entsprechen einer Knotengröße.
unnormierte Ansätze:
Die Freiwerte sind mathematische Größen und physikalisch nicht relevant. Dadurch ergeben sich einfachere Ansatzfunktionen.
Unnormierte Ansätze werden dann benutzt, wenn die Aufstellung der Ansatzfunktionen für die Kurvenfreiwerte zu aufwendig ist.
Bei diesen Ansätzen sind die Freiwerte physikalisch relevant. Sie entsprechen einer Knotengröße.
unnormierte Ansätze:
Die Freiwerte sind mathematische Größen und physikalisch nicht relevant. Dadurch ergeben sich einfachere Ansatzfunktionen.
Unnormierte Ansätze werden dann benutzt, wenn die Aufstellung der Ansatzfunktionen für die Kurvenfreiwerte zu aufwendig ist.
Ein Tragwerk ist aus duktilem Material gefertigt. Ein Versagenskriterium ist die Verglecihsspannung nach der Gestaltänderungsernergiehypothese
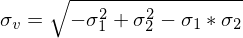
In einem kritischen Punkt des Tragwerkes herrscht
im Lastfall 1: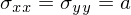
und 
und 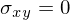im Lastfall 2: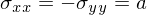
und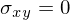
Wie hoch ist die Vergleichsspannung in beiden LAstfällen uind welcher Lastfall ist kritischer?
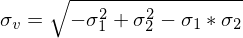
In einem kritischen Punkt des Tragwerkes herrscht
im Lastfall 1:
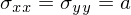und und 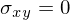im Lastfall 2:
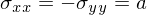und 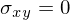Wie hoch ist die Vergleichsspannung in beiden LAstfällen uind welcher Lastfall ist kritischer?
Lastfall 1:
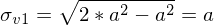
Lastfall 2:
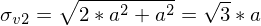
=> Lastfall 2 ist kritischer.
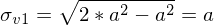
Lastfall 2:
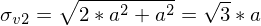
=> Lastfall 2 ist kritischer.
1. Welche Messprinzipien werden im Allgemeinen angewandt, um die Größen Druck bzw. Temperatur zu messen?
2. Was bedeutet dabei Messgrößenumformung?
2. Was bedeutet dabei Messgrößenumformung?
1.
Druck: Piezoaktoren
Temperatur: Thermoelement
2.
Messgrößenumformung: Mechanische Größen werden überwiegend elektrisch gemessen. Dazu wird die nichtelektrische,
mechanische Größe in eine proportionale elektrische Spannung oder einen Strom umgeformt.
Beim eigentlichen Messvorgang kommen dann Geräte und Verfahren zur Messung elektrischer Größen zur Anwendung.
Druck: Piezoaktoren
Temperatur: Thermoelement
2.
Messgrößenumformung: Mechanische Größen werden überwiegend elektrisch gemessen. Dazu wird die nichtelektrische,
mechanische Größe in eine proportionale elektrische Spannung oder einen Strom umgeformt.
Beim eigentlichen Messvorgang kommen dann Geräte und Verfahren zur Messung elektrischer Größen zur Anwendung.
Der folgende Schwinger ist mit 2 Dehnstabelementen (Elastizitätsmodul E, Querschnittsfläche A, Länge l, Massnedichte rho) diskretisiert.
1.
Wieviele und welche (Skizze!) Freiheitsgrade hat dieses System?
2.
Geben Sie eine Eigenfrequenz ohne Berechnung an.
3.
Geben Sie 2 Eigenvektoren ohne Berechnung an.
1.
Wieviele und welche (Skizze!) Freiheitsgrade hat dieses System?
2.
Geben Sie eine Eigenfrequenz ohne Berechnung an.
3.
Geben Sie 2 Eigenvektoren ohne Berechnung an.
1.
=> 3 FHG’s (horizontal nach rechts in jedem Lager: u1, u2, u3)
2.
ω0,1 = 0
3.
x1 = [1,1,1]
x2 = [1,0,-1]
=> 3 FHG’s (horizontal nach rechts in jedem Lager: u1, u2, u3)
2.
ω0,1 = 0
3.
x1 = [1,1,1]
x2 = [1,0,-1]
Ein schwach gedämpfter Schwinger (D=0.05) mit der technischen Eigenfrequenz von f = 5 [Hz] wird harmonisch erregt. Es interessiert die Antwort des Systems nach 0.3
s. Ein Praktikant berechnet dazu die stationäre Antwort des Systems. Was sagen sie dazu?
s. Ein Praktikant berechnet dazu die stationäre Antwort des Systems. Was sagen sie dazu?
Nach 0.3 Sekunden befindet sich der Schwinger wahrscheinlich noch in der Einschwingphase. Die stationäre Antwort des Systems wird aber erst nach abklingen der Harmonischen Schwingung (durch wegdämpfen) interessant. Dies dauert wahrscheinlich etwas länger als 0.3 s.
Ein schwach gedämpfter Einfreiheitsgradschwinger mit der ungedämpften Kreiseigenfrequenz ω0 = 10 [Hz] wird mit der Periodenkreisfrequenz Ωp = 5 [Hz] erregt. Skizzieren Sie die Vergrößerungsfunktion und begründen Sie mit Ihr, welche
Terme der Fourierreihenentwicklung zur Berechnung der stationären Antwort wichtig und welche unwichtig sind.
Terme der Fourierreihenentwicklung zur Berechnung der stationären Antwort wichtig und welche unwichtig sind.
Die folgende dreizellige doppelt symmetrische Schale ist auf Torsion beansprucht.
1.
Wievielfach statisch unbestimmt ist eine Allgemeine dreizellige Schale?
2.
Wievielfach statisch unbestimmt ist die hier dargestellte dreizellige Schale für schlaue Statiker?
3.
Wieso ist das so, und was kann man ausnützen?
4.
Zwischen den Steifen 1 und 2 tritt im Blech ein Riss auf. Statiker Schlaumann berechnet für diese Variante den Schubfluss mit einer einfachen Formel. Welche ist
das?
1.
Wievielfach statisch unbestimmt ist eine Allgemeine dreizellige Schale?
2.
Wievielfach statisch unbestimmt ist die hier dargestellte dreizellige Schale für schlaue Statiker?
3.
Wieso ist das so, und was kann man ausnützen?
4.
Zwischen den Steifen 1 und 2 tritt im Blech ein Riss auf. Statiker Schlaumann berechnet für diese Variante den Schubfluss mit einer einfachen Formel. Welche ist
das?
1.
Zweifach statisch unbestimmt
2.
Einfach statisch unbestimmt.
3.
Man kann hier die Symmetrie der Schale nutzen.
4.
Der Schubfluss zwischen 1 und 2 ist auf Grund des Risses 0! Dafür benötigt er keine Formel…
Zweifach statisch unbestimmt
2.
Einfach statisch unbestimmt.
3.
Man kann hier die Symmetrie der Schale nutzen.
4.
Der Schubfluss zwischen 1 und 2 ist auf Grund des Risses 0! Dafür benötigt er keine Formel…
Die folgende mehrzellige Schale umschließt eine Gesamtfläche von A = 1 [m2] und ist einer Torsionsbeanspruchung von MT = 2000000 [Nm] ausgesetzt
1.
Geben Sie die Zellentorsionsmomente an!
2.
Wie groß sind die Schubflüsse?
3.
Wie könnte man diese Schale vereinfachen?
1.
Geben Sie die Zellentorsionsmomente an!
2.
Wie groß sind die Schubflüsse?
3.
Wie könnte man diese Schale vereinfachen?
1.
2.
Formel von Bredt-Batho: MT = 2*A*p0
3.
Man könnte die Mittelstreben weglassen.
| MTI | MTII | MTIII | MTIV | |
| ¼ MT = 500000 | ¼ MT = 500000 | ¼ MT = 500000 | ¼ MT = 500000 |
2.
Formel von Bredt-Batho: MT = 2*A*p0
| q12 [N/m] | q23 | q34 | q41 | q15 | q25 | q35 | q45 | |
| q0/4=250000 | 250000 | 250000 | 250000 | 0 | 0 | 0 | 0 |
3.
Man könnte die Mittelstreben weglassen.
Was berechnet man mit dem Prinzip der virtuellen Verrückung und was berechnet man mit dem Prinzip der virtuellen Kräfte bzw. dem Einheitslastgesetz?
Zusatzfrage: Was besagt der Satz von Betti?
Zusatzfrage: Was besagt der Satz von Betti?
Prinzip der virtuellen Verrückung:
Äußere Arbeit = Kraft * virtuelle Verrückung
Prinzip der virtuellen Kräfte:
Äußere Arbeit = Verrückung * virtuelle Kraft
Zusatzfrage:
Äußere Arbeit = Kraft * virtuelle Verrückung
Prinzip der virtuellen Kräfte:
Äußere Arbeit = Verrückung * virtuelle Kraft
Zusatzfrage:
1.
Der dargestellte Stempel soll eine Kraft F auf einen bestimmten Bereich eines Werkstücks aufbringen. In dem FE-Modell wird dieser Bereich durch Elemente mit linearen Ansatzfunktionen modelliert. Bringen Sie die entsprechenden Kräfte in
den dargestellten Bereich an.
2.
Erläutern Sie den Unterschied zwischen einem Stabbalken und einem Biegebalken. Warum wird der Biegebalken in kommerziellen FEM-Systemen nicht verwendet?
3.
Ein System kann eine Starrkörperbewegung ausführen. Welche Bedeutung hat dies einerseits für die Steifigkeitsmatrix und andererseits für die statische
Berechnung?
Der dargestellte Stempel soll eine Kraft F auf einen bestimmten Bereich eines Werkstücks aufbringen. In dem FE-Modell wird dieser Bereich durch Elemente mit linearen Ansatzfunktionen modelliert. Bringen Sie die entsprechenden Kräfte in
den dargestellten Bereich an.
2.
Erläutern Sie den Unterschied zwischen einem Stabbalken und einem Biegebalken. Warum wird der Biegebalken in kommerziellen FEM-Systemen nicht verwendet?
3.
Ein System kann eine Starrkörperbewegung ausführen. Welche Bedeutung hat dies einerseits für die Steifigkeitsmatrix und andererseits für die statische
Berechnung?
1.
Lineare Streckenlast über alle vier Punkte, deren Summe F ergibt!
2.
Der Stabbalken besitzt 6 Freiwerte.
Der Biegebalken besitzt lediglich 4 Freiwerte.
3.
Für die Statik heißt dies, dass die Freiwerte nicht gebunden sind und somit auch keine Wechselwirkung mit anderen Freiwerten haben.
Die Steifigkeitsmatrix wird singulär:
Charakteristikum einer solchen singulären Matrix => det(K)=0
- singulär
- nicht Invertierbar
- GLS nicht Lösbar
Für die Berechnung bedeutet dies, dass die Lösung des GLS nicht möglich ist.
Lineare Streckenlast über alle vier Punkte, deren Summe F ergibt!
2.
Der Stabbalken besitzt 6 Freiwerte.
Der Biegebalken besitzt lediglich 4 Freiwerte.
3.
Für die Statik heißt dies, dass die Freiwerte nicht gebunden sind und somit auch keine Wechselwirkung mit anderen Freiwerten haben.
Die Steifigkeitsmatrix wird singulär:
Charakteristikum einer solchen singulären Matrix => det(K)=0
- singulär
- nicht Invertierbar
- GLS nicht Lösbar
Für die Berechnung bedeutet dies, dass die Lösung des GLS nicht möglich ist.
1.
Mechanisches Prinzip: Prinzip der virtuellen Arbeit (PvA)
Primäre Ergebnisse: Verschiebungen (Knotenfreiwerte)
2.
Innere Arbeit:
a: Steifigkeitsmatrix
b: virtuelle Freiwerte
c: Freiwerte
Äußere Arbeit:
d: diskretisierte Arbeit der auf das Element wirkenden Streckenlast
e+f: Ansatzfunktionen
g: Last-Vektor
h: Einzelkraft (Produkt mit virtueller Verrückung führt zur Arbeit)
3.
(a)
Beim Ableiten werden sie nicht zu null. Dies führt zu kinematischen Unverträglichkeiten beim Aufstellen der Randbedingungen.
(b)
linerare Funktion: w(x) = a0 + a1*x
quadratische Funktion: w(x) = a0 + a1*x + a2*x²
Mechanisches Prinzip: Prinzip der virtuellen Arbeit (PvA)
Primäre Ergebnisse: Verschiebungen (Knotenfreiwerte)
2.
Innere Arbeit:
a: Steifigkeitsmatrix
b: virtuelle Freiwerte
c: Freiwerte
Äußere Arbeit:
d: diskretisierte Arbeit der auf das Element wirkenden Streckenlast
e+f: Ansatzfunktionen
g: Last-Vektor
h: Einzelkraft (Produkt mit virtueller Verrückung führt zur Arbeit)
3.
(a)
Beim Ableiten werden sie nicht zu null. Dies führt zu kinematischen Unverträglichkeiten beim Aufstellen der Randbedingungen.
(b)
linerare Funktion: w(x) = a0 + a1*x
quadratische Funktion: w(x) = a0 + a1*x + a2*x²
Ein gedämpfter Schwinger wird harmonisch erregt. Die Erregung setzt bei t=0 ein. In welchem Zeitbereich spielen die Anfangsbedingungen eine Rolle? Wann kann man die stationäre Lösung als Gesamtantwort verwenden? Wie beeinflusst die Dämpfung das Verhalten?
Beim Einschwingen (t~klein) spielen die Anfangsbedingungen eine Rolle. Die stationäre Lösung kann nach dem Einschwingen (also für t~groß) als Gesamtantwort verwendet werden, da die homogene Lösung bei Dämpfung weggedämpft wird.
Je höher die Dämpfung, umso schneller verliert der homogene Teil und somit die Anfangsbedingungen Ihre Rolle.
Je höher die Dämpfung, umso schneller verliert der homogene Teil und somit die Anfangsbedingungen Ihre Rolle.
Wir betrachten einen einfachen Feder-Masse-Schwinger der krafterregt ist.
1.
Wie lautet die Kreiseigenfrequenz?
2.
Wie groß ist die stationäre Antwort für sehr kleine Ω?
3.
Wann ist die stationäre Amplitude bei p^≠0 fast null?
4.
Wann ist die stationäre Amplitude maximal?
5.
Wann ist die Phasenverschiebung der stationären Antwort π?
1.
Wie lautet die Kreiseigenfrequenz?
2.
Wie groß ist die stationäre Antwort für sehr kleine Ω?
3.
Wann ist die stationäre Amplitude bei p^≠0 fast null?
4.
Wann ist die stationäre Amplitude maximal?
5.
Wann ist die Phasenverschiebung der stationären Antwort π?
1.
Die Bewegungsgleichung lautet: m*x^..+k*x = p(t) = p^*cos(Ωt)
Aus der Standartform folgt die Eigenfrequenz: w0 = Wurzel(k/m)
2.
Die stationäre Antwort lässt sich aus der partikulären Lösung ablesen.
Ansatz:
xp(t) = p^s*p(t) = p^s*cos(Ωt)
xp(t)^. = - p^s*Ω*sin(Ωt) 1. Ableitung
xp(t)^.. = - p^s*Ω²*cos(Ωt) 2. Ableitung
einsetzen:
- m*p^s*Ω²*cos(Ωt) + k*p^s*cos(Ωt) = p^*cos(Ωt)
nach Koeffizienten auflösen:
- m*p^s*Ω² + k*p^s = p^
<=> p^s = p^/(-m*Ω² + k)
in die Ansatzfunktion einsetzen:
xp(t) = p^/(-m*Ω² + k)*cos(Ωt)
Dies stellt die stationäre Antwortamplitude dar. Für kleine Ω wird cos(~0)=1 und die Trägheit der Masse im Nenner fällt ebenfalls weg (Ω2 ~ 0).
Es folgt xp(t) = p^/k als stationäre Antwortamplitude.
3.
k => ∞
4.
Im Resonanzfall => ω0 = Ω
5.
für η > 1 d.h.
Ω/ω0 > 1 => ϕ → π
Die Bewegungsgleichung lautet: m*x^..+k*x = p(t) = p^*cos(Ωt)
Aus der Standartform folgt die Eigenfrequenz: w0 = Wurzel(k/m)
2.
Die stationäre Antwort lässt sich aus der partikulären Lösung ablesen.
Ansatz:
xp(t) = p^s*p(t) = p^s*cos(Ωt)
xp(t)^. = - p^s*Ω*sin(Ωt) 1. Ableitung
xp(t)^.. = - p^s*Ω²*cos(Ωt) 2. Ableitung
einsetzen:
- m*p^s*Ω²*cos(Ωt) + k*p^s*cos(Ωt) = p^*cos(Ωt)
nach Koeffizienten auflösen:
- m*p^s*Ω² + k*p^s = p^
<=> p^s = p^/(-m*Ω² + k)
in die Ansatzfunktion einsetzen:
xp(t) = p^/(-m*Ω² + k)*cos(Ωt)
Dies stellt die stationäre Antwortamplitude dar. Für kleine Ω wird cos(~0)=1 und die Trägheit der Masse im Nenner fällt ebenfalls weg (Ω2 ~ 0).
Es folgt xp(t) = p^/k als stationäre Antwortamplitude.
3.
k => ∞
4.
Im Resonanzfall => ω0 = Ω
5.
für η > 1 d.h.
Ω/ω0 > 1 => ϕ → π
Wann ist ein Tragwerk statisch bestimmt?
1. Wenn es äußerlich statisch bestimmt ist; d.h. wenn die Anzahl der Auflagerreaktionen gleich der Anzahl der GGW-Bedinungen ist.
2. Wenn es innerlich statisch bestimmt ist; d.h. wenn ohne aufbringen von äußerlichen Lasten keine inneren Spannungen (z.B. durch Wärmezufuhr) entstehen können.
Wenn 1. und 2. zutreffen ist das Tragwerk statisch bestimmt.
Kürzere Definition:
Wenn es möglich ist alle unbekannten Kräfte aus den Gleichgewichtsbedingungen zu berechnen. (d.h. es sind keine zusätzlichen Verformungsbedingungen nötig)
2. Wenn es innerlich statisch bestimmt ist; d.h. wenn ohne aufbringen von äußerlichen Lasten keine inneren Spannungen (z.B. durch Wärmezufuhr) entstehen können.
Wenn 1. und 2. zutreffen ist das Tragwerk statisch bestimmt.
Kürzere Definition:
Wenn es möglich ist alle unbekannten Kräfte aus den Gleichgewichtsbedingungen zu berechnen. (d.h. es sind keine zusätzlichen Verformungsbedingungen nötig)
1.
Geben Sie mit diesen Vorgaben und den hier verwendeten Symbolen die transformierte Elementensteifigkeitsmatrix an.
2.
Warum reicht es nicht aus, nur die K11-Matrix mit T11 zu transformieren?
3.
Wieso empfiehlt es sich am Knoten B keine Transformation vorzunehmen?
1.
KG = (T11^T*K11*T11 , T11^T*K12;
K21*T11 , K22)
2.
Wegen der Koppelterme, d.h. die Knoten sind nicht unabhängig.
3.
Wegen des Lagers. Ohne Transformation kann die Randbedingung frei formuliert werden. Koordinatensystem am Lager ist gleich wie das Globale.
KG = (T11^T*K11*T11 , T11^T*K12;
K21*T11 , K22)
2.
Wegen der Koppelterme, d.h. die Knoten sind nicht unabhängig.
3.
Wegen des Lagers. Ohne Transformation kann die Randbedingung frei formuliert werden. Koordinatensystem am Lager ist gleich wie das Globale.
Für ein Stabelement mit linearem Verschiebungsansatz werden die normierten
Ansatzfunktionen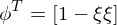
verwendet. Bestimmen Sie für eine lineare Streckenlast 
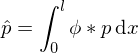_ die einzelnen Komponenten der Lastspalte.
p = [1− ξ ; ξ] * [1− ξ ξ] * [pA^ ; pB^]
Benutzen Sie dafür die normierte Koordinate ξ = x/l , ohne jedoch die Integration auszuführen.
Ansatzfunktionen
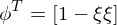verwendet. Bestimmen Sie für eine lineare Streckenlast 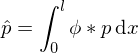_ die einzelnen Komponenten der Lastspalte.p = [1− ξ ; ξ] * [1− ξ ξ] * [pA^ ; pB^]
Benutzen Sie dafür die normierte Koordinate ξ = x/l , ohne jedoch die Integration auszuführen.
Was versteht man unter modaler Analyse (Weg, Vorteile, Nachteile)?
Zurückführung von Mehrfreiheitsgradschwingern auf Einfreiheitsgradschwingern.
Weg:
Vorteile:
- Komplexe Systeme können so einfacher analysiert werden.
- Zur Bestimmung der Übertragungsmatrix ist keine Matrizeninversion mehr nötig
- Polstellen können direkt abgelesen werden.
- lässt Vernachlässigung höherer Mode sehr einfach durch sortieren nach Frequenzen zu
Nachteile:
Bei Gedämpften System diagonalisieren die eigenvektoren des ungedämpften Systems nicht mehr zwangsläufig die Dämpfungsmatrix D.
=> Keine oder nur umständliche Erfassung der Dämpfung!
Weg:
Vorteile:
- Komplexe Systeme können so einfacher analysiert werden.
- Zur Bestimmung der Übertragungsmatrix ist keine Matrizeninversion mehr nötig
- Polstellen können direkt abgelesen werden.
- lässt Vernachlässigung höherer Mode sehr einfach durch sortieren nach Frequenzen zu
Nachteile:
Bei Gedämpften System diagonalisieren die eigenvektoren des ungedämpften Systems nicht mehr zwangsläufig die Dämpfungsmatrix D.
=> Keine oder nur umständliche Erfassung der Dämpfung!
Flashcard set info:
Author: carrera-911
Main topic: Bauingenieurwesen
Topic: ISD
Published: 19.03.2010
Card tags:
All cards (27)
no tags
